Variational and Topological Methods: Theory, Applications,
Numerical Simulations, and Open Problems.
Electron. J. Diff. Eqns., Conference 21 (2014), pp. 223-234.
Extinction of weak solutions of doubly nonlinear Navier-Stokes equations
Jochen Merker
Abstract:
In this article we discus the doubly nonlinear incompressible
Navier-Stokes equations
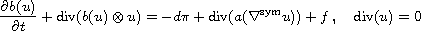
are discussed, where u models the velocity vector field
of a homogeneous incompressible non-Newtonian fluid
whose momentum
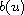 depends nonlinearly on u.
Particularly, under certain regularity assumptions it is shown
that u becomes extinct in finite time
for sufficiently small initial values u(0), if
depends nonlinearly on u.
Particularly, under certain regularity assumptions it is shown
that u becomes extinct in finite time
for sufficiently small initial values u(0), if
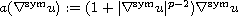 and
and
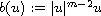 with
with
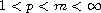 I.
I.
Published February 10, 2014.
Math Subject Classifications: 58F15, 58F17, 53C35.
Key Words: Navier-Stokes equations; doubly nonlinear evolution equations;
extinction.
Show me the PDF(287 K),
TEX and other files for this article.
 |
Jochen Merker
Universitäat Rostock - Institut für Mathematik
Ulmenstr. 69 (Haus 3)
18057 Rostock, Germany
email: jochen.merker@uni-rostock.de
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
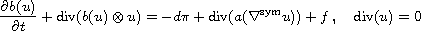
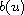 depends nonlinearly on u.
Particularly, under certain regularity assumptions it is shown
that u becomes extinct in finite time
for sufficiently small initial values u(0), if
depends nonlinearly on u.
Particularly, under certain regularity assumptions it is shown
that u becomes extinct in finite time
for sufficiently small initial values u(0), if
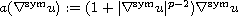 and
and
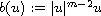 with
with
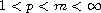 I.
I.
