p-trigonometric functions are generalizations of the trigonometric functions. They appear in context of nonlinear differential equations and also in analytical geometry of the p-circle in the plain. The most important p-trigonometric function is
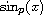 .
For p>1, this function is defined as the unique solution
of the initial-value problem
.
For p>1, this function is defined as the unique solution
of the initial-value problem

for any
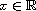 .
We prove that the
.
We prove that the
 -th derivative of
-th derivative of
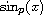 can be expressed in the form
can be expressed in the form
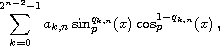
on
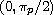 , where
, where
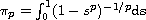 ,
and
,
and
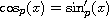 .
Using this formula, we proved the order of differentiability
of the function
.
Using this formula, we proved the order of differentiability
of the function
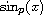 .
The most surprising (least expected)
result is that
.
The most surprising (least expected)
result is that
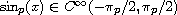 if p is an even integer.
This result was essentially used in the proof of theorem, which says that the
Maclaurin series of
if p is an even integer.
This result was essentially used in the proof of theorem, which says that the
Maclaurin series of
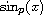 converges on
converges on
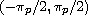 if
p is an even integer. This completes previous results that were
known e.g. by Lindqvist and Peetre where this convergence was conjectured.
if
p is an even integer. This completes previous results that were
known e.g. by Lindqvist and Peetre where this convergence was conjectured.

