Variational and Topological Methods: Theory, Applications,
Numerical Simulations, and Open Problems.
Electron. J. Diff. Eqns., Conference 21 (2014), pp. 11-21
A model problem for ultrafunctions
Vieri Benci, Lorenzo Luperi Baglini
Abstract:
In this article. we show that non-Archimedean mathematics (NAM),
namely mathematics which uses infinite and infinitesimal numbers,
is useful to model some physical problems which cannot be described
by the usual mathematics. The problem which we will consider here
is the minimization of the functional
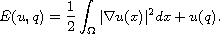
When
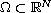 is a bounded open set and
is a bounded open set and
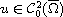 , this problem has no
solution since
, this problem has no
solution since
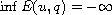 .
On the contrary, as we will show,
this problem is well posed in a suitable non-Archimedean frame.
More precisely, we apply the general ideas of NAM and some of the
techniques of Non Standard Analysis to a new notion of generalized functions,
called ultrafunctions, which are a particular class of functions based on a
Non-Archimedean field. In this class of functions, the above problem
is well posed and it has a solution.
.
On the contrary, as we will show,
this problem is well posed in a suitable non-Archimedean frame.
More precisely, we apply the general ideas of NAM and some of the
techniques of Non Standard Analysis to a new notion of generalized functions,
called ultrafunctions, which are a particular class of functions based on a
Non-Archimedean field. In this class of functions, the above problem
is well posed and it has a solution.
Published February 10, 2014.
Math Subject Classifications: 26E30, 26E35, 35D99, 35J57.
Key Words: Non Archimedean mathematics; non standard analysis;
ultrafunctions; delta function; Dirichlet problem.
Show me the PDF(236 K),
TEX and other files for this article.
 |
Vieri Benci
Dipartimento di Matematica
Università degli Studi di Pisa
Via F. Buonarroti 1/c, Pisa, Italy
email: benci@dma.unipi.it
|
|---|
 |
Lorenzo Luperi Baglini
University of Vienna, Faculty of Mathematics
Oskar-Morgenstern-Platz 1
1090 Vienna, Austria
email: lorenzo.luperi.baglini@univie.ac.at
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
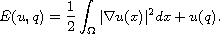
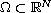 is a bounded open set and
is a bounded open set and
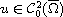 , this problem has no
solution since
, this problem has no
solution since
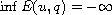 .
On the contrary, as we will show,
this problem is well posed in a suitable non-Archimedean frame.
More precisely, we apply the general ideas of NAM and some of the
techniques of Non Standard Analysis to a new notion of generalized functions,
called ultrafunctions, which are a particular class of functions based on a
Non-Archimedean field. In this class of functions, the above problem
is well posed and it has a solution.
.
On the contrary, as we will show,
this problem is well posed in a suitable non-Archimedean frame.
More precisely, we apply the general ideas of NAM and some of the
techniques of Non Standard Analysis to a new notion of generalized functions,
called ultrafunctions, which are a particular class of functions based on a
Non-Archimedean field. In this class of functions, the above problem
is well posed and it has a solution.

