Ninth MSU-UAB Conference on Differential Equations and Computational Simulations.
Electron. J. Diff. Eqns., Conference 20 (2013), pp. 15-25.
S-shaped bifurcation curves for logistic growth and
weak Allee effect growth models with grazing on an interior patch
Dagny Butler, Ratnasingham Shivaji, Anna Tuck
Abstract:
We study the positive solutions to the steady state reaction
diffusion equations with Dirichlet boundary conditions of the form
![$$\displaylines{
-u''= \cases{
\lambda[u - \frac{1}{K}u^2 - c \frac{u^2}{1+u^2}], & $x \in (L,1-L)$,\cr
\lambda[u - \frac{1}{K}u^2], & $x \in (0,L)\cup(1-L,1)$,
} \cr
u(0)=0, \quad u(1)=0
}$$](gifs/aa.gif)
and
![$$\displaylines{
-u''= \cases{
\lambda[u(u+1)(b-u) - c \frac{u^2}{1+u^2}], & $x \in (L,1-L)$, \cr
\lambda[u(u+1)(b-u)], & $x \in (0,L)\cup(1-L,1)$,
} \cr
u(0)=0,\quad u(1)=0.
}$$](gifs/ab.gif)
Here,
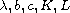 are positive constants with
0<L<1/2. These types of steady state equations occur in
population dynamics; the first model describes logistic growth with grazing,
and the second model describes weak Allee effect with grazing.
In both cases, u is the population density,
are positive constants with
0<L<1/2. These types of steady state equations occur in
population dynamics; the first model describes logistic growth with grazing,
and the second model describes weak Allee effect with grazing.
In both cases, u is the population density,
 is the diffusion coefficient, and c is the maximum grazing rate.
These models correspond to the case of symmetric grazing on an interior region.
Our goal is to study the existence of positive solutions. Previous studies
when the grazing was throughout the domain resulted in S-shaped bifurcation
curves for certain parameter ranges. Here, we show that such S-shaped
bifurcations occur even if the grazing is confined to the interior.
We discuss the results via a modified quadrature method and
Mathematica computations.
is the diffusion coefficient, and c is the maximum grazing rate.
These models correspond to the case of symmetric grazing on an interior region.
Our goal is to study the existence of positive solutions. Previous studies
when the grazing was throughout the domain resulted in S-shaped bifurcation
curves for certain parameter ranges. Here, we show that such S-shaped
bifurcations occur even if the grazing is confined to the interior.
We discuss the results via a modified quadrature method and
Mathematica computations.
Published October 31, 2013.
Math Subject Classifications: 34B18.
Key Words: Grazing on an interior patch; positive solutions;
S-shaped bifurcation curves.
Show me the PDF file (1034 K),
TEX file, and other files for this article.
 |
Dagny Butler
Department of Mathematics & Statistics
Mississippi State University
Mississippi State, MS 39762, USA
email: dlgrilli@uncg.edu, dg301@msstate.edu
|
|---|
 |
Ratnasingham Shivaji
Department of Mathematics & Statistics
University of North Carolina at Greensboro
Greensboro, NC 27412, USA
email: shivaji@uncg.edu
|
 |
Anna Tuck
Department of Mathematics & Statistics
University of North Carolina at Greensboro
Greensboro, NC 27412, USA
email: avtuck@uncg.edu
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
![$$\displaylines{
-u''= \cases{
\lambda[u - \frac{1}{K}u^2 - c \frac{u^2}{1+u^2}], & $x \in (L,1-L)$,\cr
\lambda[u - \frac{1}{K}u^2], & $x \in (0,L)\cup(1-L,1)$,
} \cr
u(0)=0, \quad u(1)=0
}$$](gifs/aa.gif)
![$$\displaylines{
-u''= \cases{
\lambda[u(u+1)(b-u) - c \frac{u^2}{1+u^2}], & $x \in (L,1-L)$, \cr
\lambda[u(u+1)(b-u)], & $x \in (0,L)\cup(1-L,1)$,
} \cr
u(0)=0,\quad u(1)=0.
}$$](gifs/ab.gif)
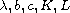 are positive constants with
0<L<1/2. These types of steady state equations occur in
population dynamics; the first model describes logistic growth with grazing,
and the second model describes weak Allee effect with grazing.
In both cases, u is the population density,
are positive constants with
0<L<1/2. These types of steady state equations occur in
population dynamics; the first model describes logistic growth with grazing,
and the second model describes weak Allee effect with grazing.
In both cases, u is the population density,
 is the diffusion coefficient, and c is the maximum grazing rate.
These models correspond to the case of symmetric grazing on an interior region.
Our goal is to study the existence of positive solutions. Previous studies
when the grazing was throughout the domain resulted in S-shaped bifurcation
curves for certain parameter ranges. Here, we show that such S-shaped
bifurcations occur even if the grazing is confined to the interior.
We discuss the results via a modified quadrature method and
Mathematica computations.
is the diffusion coefficient, and c is the maximum grazing rate.
These models correspond to the case of symmetric grazing on an interior region.
Our goal is to study the existence of positive solutions. Previous studies
when the grazing was throughout the domain resulted in S-shaped bifurcation
curves for certain parameter ranges. Here, we show that such S-shaped
bifurcations occur even if the grazing is confined to the interior.
We discuss the results via a modified quadrature method and
Mathematica computations.


