Eighth Mississippi State - UAB Conference on Differential Equations
and Computational Simulations.
Electron. J. Diff. Eqns., Conference 19 (2010), pp. 245-255.
Bifurcation of solutions of separable parameterized
equations into lines
Yun-Qiu Shen, Tjalling J. Ypma
Abstract:
Many applications give rise to separable parameterized equations
of the form
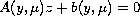 , where
, where
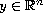 ,
,
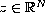 and the parameter
and the parameter
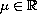 ;
here
;
here
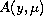 is an
is an
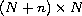 matrix and
matrix and
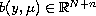 .
Under the assumption that
.
Under the assumption that
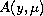 has full rank we showed in [21] that
bifurcation points can be located by solving a reduced equation
of the form
has full rank we showed in [21] that
bifurcation points can be located by solving a reduced equation
of the form
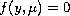 .
In this paper we extend that method
to the case that
.
In this paper we extend that method
to the case that
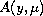 has rank deficiency one at the
bifurcation point. At such a point the solution curve
has rank deficiency one at the
bifurcation point. At such a point the solution curve
 branches into infinitely many additional solutions, which form
a straight line. A numerical method for reducing the problem to a
smaller space and locating such a bifurcation point is given.
Applications to equilibrium solutions of nonlinear ordinary
equations and solutions of discretized partial differential
equations are provided.
branches into infinitely many additional solutions, which form
a straight line. A numerical method for reducing the problem to a
smaller space and locating such a bifurcation point is given.
Applications to equilibrium solutions of nonlinear ordinary
equations and solutions of discretized partial differential
equations are provided.
Published September 25, 2010.
Math Subject Classifications: 65P30, 65H10, 34C23, 37G10.
Key Words: Separable parameterized equations; bifurcation; rank deficiency;
Golub-Pereyra variable projection method; bordered matrix;
singular value decomposition; Newton's method.
Show me the PDF file (248K),
TEX file, and other files for this article.
 |
Yun-Qiu Shen
Department of Mathematics,
Western Washington University
Bellingham, WA 98225-9063, USA
email: yunqiu.shen@wwu.edu
|
|---|
 |
Tjalling J. Ypma
Department of Mathematics,
Western Washington University
Bellingham, WA 98225-9063, USA
email: tjalling.ypma@wwu.edu
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
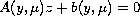 , where
, where
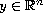 ,
,
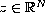 and the parameter
and the parameter
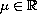 ;
here
;
here
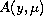 is an
is an
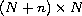 matrix and
matrix and
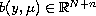 .
Under the assumption that
.
Under the assumption that
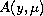 has full rank we showed in [21] that
bifurcation points can be located by solving a reduced equation
of the form
has full rank we showed in [21] that
bifurcation points can be located by solving a reduced equation
of the form
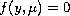 .
In this paper we extend that method
to the case that
.
In this paper we extend that method
to the case that
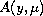 has rank deficiency one at the
bifurcation point. At such a point the solution curve
has rank deficiency one at the
bifurcation point. At such a point the solution curve
 branches into infinitely many additional solutions, which form
a straight line. A numerical method for reducing the problem to a
smaller space and locating such a bifurcation point is given.
Applications to equilibrium solutions of nonlinear ordinary
equations and solutions of discretized partial differential
equations are provided.
branches into infinitely many additional solutions, which form
a straight line. A numerical method for reducing the problem to a
smaller space and locating such a bifurcation point is given.
Applications to equilibrium solutions of nonlinear ordinary
equations and solutions of discretized partial differential
equations are provided.

