Eighth Mississippi State - UAB Conference on Differential Equations
and Computational Simulations.
Electron. J. Diff. Eqns., Conference 19 (2010), pp. 189-196.
Comparison of time stepping schemes on the cable equation
Chuan Li, Vasilios Alexiades
Abstract:
Electrical propagation in excitable tissue, such as nerve
fibers and heart muscle, is described by a parabolic PDE
for the transmembrane voltage
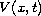 ,
known as the cable equation,
,
known as the cable equation,
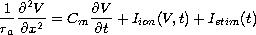
where
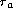 and
and
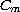 are the axial resistance and membrane
capacitance. The source term
are the axial resistance and membrane
capacitance. The source term
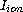 represents the total ionic
current across the membrane, governed by the Hodgkin-Huxley or other
more complicated ionic models.
represents the total ionic
current across the membrane, governed by the Hodgkin-Huxley or other
more complicated ionic models.
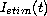 is an applied stimulus
current.
is an applied stimulus
current.
We compare the performance of various low and high order
time-stepping numerical schemes, including DuFort-Frankel
and adaptive Runge-Kutta, on the 1D cable equation.
Published September 25, 2010.
Math Subject Classifications: 65M08, 35K57, 92C37.
Key Words: Explicit schemes; super time stepping; adaptive Runge Kutta;
Dufort Frankel; action potential; Luo-Rudy ionic models.
Show me the PDF file (251K),
TEX file, and other files for this article.
 |
Chuan Li
Mathematics Department, University of Tennessee
Knoxville TN 37996, USA
email: li@math.utk.edu
|
|---|
 |
Vasilios Alexiades
Mathematics Department, University of Tennessee
Knoxville TN 37996, USA
email: alexiades@utk.edu
|
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
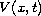 ,
known as the cable equation,
,
known as the cable equation,
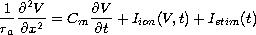
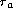 and
and
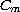 are the axial resistance and membrane
capacitance. The source term
are the axial resistance and membrane
capacitance. The source term
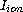 represents the total ionic
current across the membrane, governed by the Hodgkin-Huxley or other
more complicated ionic models.
represents the total ionic
current across the membrane, governed by the Hodgkin-Huxley or other
more complicated ionic models.
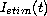 is an applied stimulus
current.
is an applied stimulus
current.

