Seventh Mississippi State - UAB Conference on Differential Equations and
Computational Simulations.
Electron. J. Diff. Eqns., Conference 17 (2009), pp. 133-148.
A multilevel adaptive mesh generation scheme using Kd-trees
Alfonso Limon, Hedley Morris
Abstract:
We introduce a mesh refinement strategy for PDE based simulations
that benefits from a multilevel decomposition. Using Harten's MRA
in terms of Schroder-Pander linear multiresolution analysis
[20], we are able to bound discontinuities in
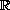 .
This MRA is extended to
.
This MRA is extended to
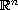 in terms
of n-orthogonal linear transforms and utilized to identify cells
that contain a codimension-one discontinuity. These refinement
cells become leaf nodes in a balanced Kd-tree such that a
local dyadic MRA is produced in
in terms
of n-orthogonal linear transforms and utilized to identify cells
that contain a codimension-one discontinuity. These refinement
cells become leaf nodes in a balanced Kd-tree such that a
local dyadic MRA is produced in
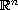 ,
while maintaining
a minimal computational footprint. The nodes in the tree form an
adaptive mesh whose density increases in the vicinity of a discontinuity.
,
while maintaining
a minimal computational footprint. The nodes in the tree form an
adaptive mesh whose density increases in the vicinity of a discontinuity.
Published April 15, 2009.
Math Subject Classifications:
Key Words: Adaptive grid refinement; Wavelet refined mesh; quadtree grids;
multilevel decomposition; codimension-one discontinuities.
Show me the PDF file (568 KB),
TEX file, and other files for this article.
 |
Alfonso Limon
School of Mathematical Sciences
Claremont Graduate University, CA 91711, USA
email: alfonso.limon@cgu.edu
|
|---|
 |
Hedley Morris
School of Mathematical Sciences
Claremont Graduate University, CA 91711, USA
email: hedley.morris@cgu.edu |
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
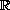 .
This MRA is extended to
.
This MRA is extended to
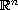 in terms
of n-orthogonal linear transforms and utilized to identify cells
that contain a codimension-one discontinuity. These refinement
cells become leaf nodes in a balanced Kd-tree such that a
local dyadic MRA is produced in
in terms
of n-orthogonal linear transforms and utilized to identify cells
that contain a codimension-one discontinuity. These refinement
cells become leaf nodes in a balanced Kd-tree such that a
local dyadic MRA is produced in
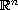 ,
while maintaining
a minimal computational footprint. The nodes in the tree form an
adaptive mesh whose density increases in the vicinity of a discontinuity.
,
while maintaining
a minimal computational footprint. The nodes in the tree form an
adaptive mesh whose density increases in the vicinity of a discontinuity.

