Seventh Mississippi State - UAB Conference on Differential Equations and
Computational Simulations.
Electron. J. Diff. Eqns., Conference 17 (2009), pp. 123-131.
Subsolutions: A journey from positone to infinite semipositone problems
Eun Kyoung Lee, Ratnasingham Shivaji, Jinglong Ye
Abstract:
We discuss the existence of positive solutions to
 in
in
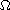 , with
, with
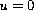 on the boundary, where
on the boundary, where
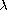 is a positive parameter,
is a positive parameter,
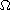 is a bounded domain with smooth boundary
is a bounded domain with smooth boundary
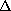 is the Laplacian operator, and
is the Laplacian operator, and
 is a continuous function. We first
discuss the cases when
is a continuous function. We first
discuss the cases when
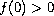 (positone),
(positone),
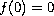 and
and
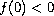 (semipositone). In particular, we will review the existence of
non-negative strict subsolutions. Along with these subsolutions and
appropriate assumptions on
(semipositone). In particular, we will review the existence of
non-negative strict subsolutions. Along with these subsolutions and
appropriate assumptions on
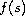 for
for
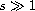 (which will lead to
large supersolutions) we discuss the existence of positive
solutions. Finally, we obtain new results on the case of infinite
semipositone problems
(
(which will lead to
large supersolutions) we discuss the existence of positive
solutions. Finally, we obtain new results on the case of infinite
semipositone problems
(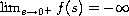 ).
).
Published April 15, 2009.
Math Subject Classifications: 35J25.
Key Words: Positone; semipositone; infinite semipositone;
sub-super solutions.
Show me the PDF file (226 KB),
TEX file, and other files for this article.
 |
Eun Kyoung Lee
Department of Mathematics and Statistics, Center for
Computational Sciences
Mississippi State University, Mississippi State, MS 39762, USA
email: el165@msstate.edu |
|---|
 |
Ratnasingham Shivaji
Department of Mathematics and Statistics, Center
for Computational Sciences
Mississippi State University,
Mississippi State, MS 39762, USA
email: shivaji@ra.msstate.edu |
|---|
 |
Jinglong Ye
Department of Mathematics and Statistics,
Mississippi State University
Mississippi State, MS 39762, USA
email: jy79@msstate.edu |
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
 in
in
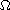 , with
, with
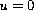 on the boundary, where
on the boundary, where
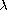 is a positive parameter,
is a positive parameter,
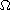 is a bounded domain with smooth boundary
is a bounded domain with smooth boundary
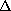 is the Laplacian operator, and
is the Laplacian operator, and
 is a continuous function. We first
discuss the cases when
is a continuous function. We first
discuss the cases when
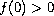 (positone),
(positone),
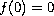 and
and
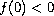 (semipositone). In particular, we will review the existence of
non-negative strict subsolutions. Along with these subsolutions and
appropriate assumptions on
(semipositone). In particular, we will review the existence of
non-negative strict subsolutions. Along with these subsolutions and
appropriate assumptions on
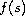 for
for
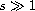 (which will lead to
large supersolutions) we discuss the existence of positive
solutions. Finally, we obtain new results on the case of infinite
semipositone problems
(
(which will lead to
large supersolutions) we discuss the existence of positive
solutions. Finally, we obtain new results on the case of infinite
semipositone problems
(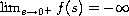 ).
).


