

Benedicte Alziary, Peter Takac
Abstract:
We investigate the compactness of the resolvent
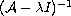 of the Schrodinger operator
of the Schrodinger operator
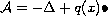 acting on the Banach space
acting on the Banach space
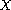 ,
,
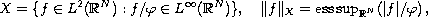
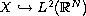 , where
, where
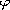 denotes
the ground state for
denotes
the ground state for
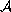 acting on
acting on
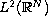 .
The potential
.
The potential
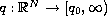 , bounded from below,
is a "relatively small" perturbation of a radially symmetric potential
which is assumed to be monotone increasing
(in the radial variable) and growing somewhat faster than
, bounded from below,
is a "relatively small" perturbation of a radially symmetric potential
which is assumed to be monotone increasing
(in the radial variable) and growing somewhat faster than
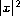 as
as
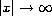 .
If
.
If
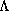 is the ground state energy for
is the ground state energy for
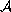 ,
i.e.
,
i.e.
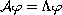 ,
we show that the operator
,
we show that the operator
 is not only bounded, but also compact for
is not only bounded, but also compact for
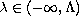 .
In particular, the spectra of
.
In particular, the spectra of
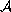 in
in
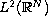 and
and
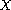 coincide; each eigenfunction of
coincide; each eigenfunction of
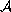 belongs to
belongs to
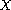 ,
i.e., its absolute value is bounded by
,
i.e., its absolute value is bounded by
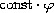 .
.
Published May 15, 2007.
Math Subject Classifications: 47A10, 35J10, 35P15, 81Q15.
Key Words: Ground-state space; compact resolvent; Schrodinger operator;
monotone radial potential; maximum and anti-maximum principle;
comparison of ground states; asymptotic equivalence.
Show me the PDF file (414K), TEX file, and other files for this article.
 |
Bénédicte Alziary CEREMATH - UMR MIP Université Toulouse 1 (Sciences Sociales) 21 Allées de Brienne, F-31000 Toulouse Cedex, France email: alziary@univ-tlse1.fr |
|---|---|
 |
Peter Takác Institut für Mathematik, Universität Rostock Universitätsplatz 1, D-18055 Rostock, Germany email: peter.takac@uni-rostock.de |
Return to the table of contents
for this conference.
Return to the EJDE web page