2006 International Conference in honor of Jacqueline Fleckinger.
Electron. J. Diff. Eqns., Conference 16 (2007), pp. 29-34.
On positive solutions for a class of
strongly coupled p-Laplacian systems
Jaffar Ali, R. Shivaji
Abstract:
Consider the system
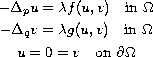
where
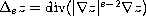 ,
,
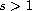 ,
,
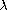 is a non-negative parameter, and
is a non-negative parameter, and
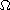 is a bounded
domain in
is a bounded
domain in
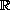 with smooth boundary
with smooth boundary
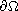 . We
discuss the existence of a large positive solution for
. We
discuss the existence of a large positive solution for
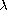 large when
large when
![$$
\lim_{x\to\infty}\frac{f(x,M[g(x,x)]^{1/q-1})}{x^{p-1}}=0
$$](gifs/ai.gif)
for every
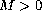 ,
and
,
and
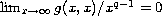 . In
particular, we do not assume any sign conditions on
. In
particular, we do not assume any sign conditions on
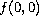 or
or
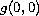 .
We also discuss a multiplicity results when
.
We also discuss a multiplicity results when
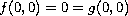 .
.
Published May 15, 2007.
Math Subject Classifications: 35J55, 35J70.
Key Words: Positive solutions; p-Laplacian systems;
semipositone problems.
Show me the
PDF file (190K),
TEX file, and other files for this article.
 |
Jaffar Ali
Department of Mathematics
Mississippi State University
Mississippi State, MS 39759, USA
email: js415@ra.msstate.edu |
|---|
 |
Ratnasingham Shivaji
Department of Mathematics
Mississippi State University
Mississippi State, MS 39759, USA
email: shivaji@ra.msstate.edu |
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
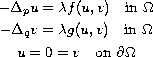
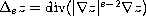 ,
,
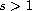 ,
,
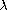 is a non-negative parameter, and
is a non-negative parameter, and
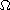 is a bounded
domain in
is a bounded
domain in
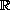 with smooth boundary
with smooth boundary
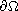 . We
discuss the existence of a large positive solution for
. We
discuss the existence of a large positive solution for
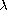 large when
large when
![$$
\lim_{x\to\infty}\frac{f(x,M[g(x,x)]^{1/q-1})}{x^{p-1}}=0
$$](gifs/ai.gif)
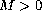 ,
and
,
and
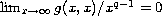 . In
particular, we do not assume any sign conditions on
. In
particular, we do not assume any sign conditions on
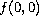 or
or
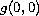 .
We also discuss a multiplicity results when
.
We also discuss a multiplicity results when
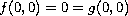 .
.

