Sixth Mississippi State Conference on Differential Equations and
Computational Simulations.
Electron. J. Diff. Eqns., Conference 15 (2007), pp. 239-249.
On the exact multiplicity of solutions for boundary-value
problems via computing the direction of bifurcations
Joaquin Rivera, Yi Li
Abstract:
We consider positive solutions of the Dirichlet problem
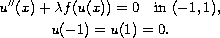
depending on a positive parameter
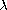 .
We use two formulas derived in
[18] to compute all solutions
.
We use two formulas derived in
[18] to compute all solutions
 where a turn may occur and to
compute the direction of the turn. As an application, we consider quintic a
polynomial
where a turn may occur and to
compute the direction of the turn. As an application, we consider quintic a
polynomial
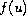 with positive and distinct roots. For such quintic
polynomials we conjecture the exact mutiplicity structure of positive
solutions and present computer assisted proofs of such exact bifurcation
diagrams for various distributions of the real roots. The limiting behavior
of the solutions on these bifurcation branches as
with positive and distinct roots. For such quintic
polynomials we conjecture the exact mutiplicity structure of positive
solutions and present computer assisted proofs of such exact bifurcation
diagrams for various distributions of the real roots. The limiting behavior
of the solutions on these bifurcation branches as
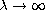 and
their stabilities are also investigated.
and
their stabilities are also investigated.
Published February 28, 2007.
Math Subject Classifications: 34B15.
Key Words: Bifurcation points; direction of the turn; multiplicity of solutions.
Show me the
PDF file (252K),
TEX file, and other files for this article.
 |
Joaquin Rivera
Department of Mathematics,
University of Iowa
Iowa City, Iowa 52242, USA
email: rvera@math.uiowa.edu |
|---|
 |
Yi Li
Department of Mathematics,
University of Iowa
Iowa City, Iowa 52242, USA.
Hunan Normal University
Changsha 410081, Hunan, China
email: yi-li@uiowa.edu |
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
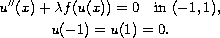
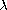 .
We use two formulas derived in
[18] to compute all solutions
.
We use two formulas derived in
[18] to compute all solutions
 where a turn may occur and to
compute the direction of the turn. As an application, we consider quintic a
polynomial
where a turn may occur and to
compute the direction of the turn. As an application, we consider quintic a
polynomial
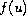 with positive and distinct roots. For such quintic
polynomials we conjecture the exact mutiplicity structure of positive
solutions and present computer assisted proofs of such exact bifurcation
diagrams for various distributions of the real roots. The limiting behavior
of the solutions on these bifurcation branches as
with positive and distinct roots. For such quintic
polynomials we conjecture the exact mutiplicity structure of positive
solutions and present computer assisted proofs of such exact bifurcation
diagrams for various distributions of the real roots. The limiting behavior
of the solutions on these bifurcation branches as
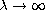 and
their stabilities are also investigated.
and
their stabilities are also investigated.

