We study the existence of solutions for the generalized multi-point boundary-value problem
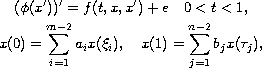
in the non-resonance case. Our methods consist in using topological degree and some a priori estimates.
Chaitan P. Gupta
Abstract:
We study the existence of solutions for the generalized multi-point
boundary-value problem
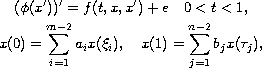
in the non-resonance case.
Our methods consist in using topological degree and some a priori estimates.
Published February 28, 2007.
Math Subject Classifications: 34B10, 34B15, 34L30, 34L90.
Key Words: Generalized multi-point boundary value problems;
p-Laplace type operator, non-resonance;
a priori estimates; topological degree.
Show me the PDF file (252K), TEX file, and other files for this article.
 |
Chaitan P. Gupta Department of Mathematics 084 University of Nevada, Reno Reno, NV 89557, USA email: gupta@unr.edu |
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page