Sixth Mississippi State Conference on Differential Equations and
Computational Simulations.
Electron. J. Diff. Eqns., Conference 15 (2007), pp. 97-106.
A pattern formation problem on the sphere
Clara E. Garza-Hume, Pablo Padilla
Abstract:
We consider a semi-linear elliptic equation on the sphere
 with
with
 odd and
subcritical nonlinearity. We show that given any positive
integer
odd and
subcritical nonlinearity. We show that given any positive
integer
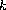 ,
if the exponent
,
if the exponent
 of the nonlinear term
is sufficiently close to the critical Sobolev exponent
of the nonlinear term
is sufficiently close to the critical Sobolev exponent
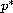 ,
then there exists a positive solution with
,
then there exists a positive solution with
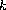 peaks. Moreover,
the minimum energy solutions with
peaks. Moreover,
the minimum energy solutions with
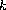 peaks are such that the centers
of these concentrations converge as
peaks are such that the centers
of these concentrations converge as
 to the solution of
an underlying geometrical problem, namely,
arranging
to the solution of
an underlying geometrical problem, namely,
arranging
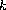 points on
points on
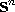 so they are as far away
from each other as possible.
so they are as far away
from each other as possible.
Published February 28, 2007.
Math Subject Classifications: 35B33, 35J20.
Key Words: Semilinear elliptic equation; sphere packing;
critical Sobolev exponent; pattern formation.
Show me the
PDF file (257K),
TEX file, and other files for this article.
 |
Clara E. Garza-Hume
IIMAS-FENOMEC, Universidad Nacional Autónoma de México
Circuito Escolar, Cd. Universitaria 04510
México D. F., México
email: clara@mym.iimas.unam.mx |
|---|
 |
Pablo Padilla
IIMAS-FENOMEC, Universidad Nacional Autónoma de México
Circuito Escolar, Cd. Universitaria 04510
México D. F., México
email: pablo@mym.iimas.unam.mx |
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page
 with
with
 odd and
subcritical nonlinearity. We show that given any positive
integer
odd and
subcritical nonlinearity. We show that given any positive
integer
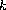 ,
if the exponent
,
if the exponent
 of the nonlinear term
is sufficiently close to the critical Sobolev exponent
of the nonlinear term
is sufficiently close to the critical Sobolev exponent
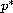 ,
then there exists a positive solution with
,
then there exists a positive solution with
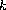 peaks. Moreover,
the minimum energy solutions with
peaks. Moreover,
the minimum energy solutions with
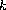 peaks are such that the centers
of these concentrations converge as
peaks are such that the centers
of these concentrations converge as
 to the solution of
an underlying geometrical problem, namely,
arranging
to the solution of
an underlying geometrical problem, namely,
arranging
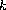 points on
points on
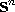 so they are as far away
from each other as possible.
so they are as far away
from each other as possible.

