In this paper we prove existence and uniqueness of classical solutions for the non-autonomous inhomogeneous Cauchy problem
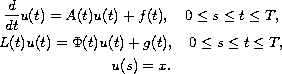
The solution to this problem is obtained by a variation of constants formula.
Mohammed Filali, Belhadj Karim
Abstract:
In this paper we prove existence and uniqueness of
classical solutions for the non-autonomous inhomogeneous
Cauchy problem
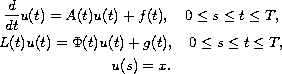
The solution to this problem is obtained by a variation of
constants formula.
Published September 20, 2006.
Math Subject Classifications: 34G10, 47D06.
Key Words: Boundary Cauchy problem; evolution families; solution;
well posedness; variation of constants formula.
Show me the PDF file (231K), TEX file, and other files for this article.
 |
Mohammed Filali Département de Mathématiques et Informatique Faculté des Sciences Université Mohammed 1er, Oujda, Maroc email: filali@sciences.univ-oujda.ac.ma |
|---|---|
 |
Belhadj Karim Département de Mathématiques et Informatique Faculté des Sciences Université Mohammed 1er, Oujda, Maroc email: karim@sciences.univ-oujda.ac.ma |
Return to the table of contents for this conference.
Return to the EJDE web page