2005-Oujda International Conference on Nonlinear Analysis,
Oujda, Morocco.
Electron. J. Diff. Eqns., Conference 14 (2006), pp. 135-147.
Optimal controls for a class of nonlinear evolution systems
Abdelhaq Benbrik, Mohammed Berrajaa, Samir Lahrech
Abstract:
We consider the abstract nonlinear evolution equation
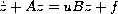 .
Viewing
.
Viewing
 as control,
we seek to minimize
as control,
we seek to minimize
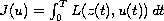 .
Under suitable hypotheses, it is shown that there exists an
optimal control
.
Under suitable hypotheses, it is shown that there exists an
optimal control
 and that it satisfies the
appropriate optimality system. An example involving the
and that it satisfies the
appropriate optimality system. An example involving the
 -Laplacian
operator demonstrates the applicability of our results.
-Laplacian
operator demonstrates the applicability of our results.
Published September 20, 2006.
Math Subject Classifications: 49J20, 49K20.
Key Words: Optimal control; monotone operator; compact embedding;
$p$-Laplacian; bilinear system.
Show me the
PDF file (248K),
TEX file, and other files for this article.
 |
Abdelhaq Benbrik
Département de Mathématiques et Informatique
Faculté des Sciences
Université Mohammed 1er, Oujda, Maroc
email: benbrik@sciences.univ-oujda.ac.ma |
|---|
 |
Mohammed Berrajaa
Département de Mathématiques et Informatique
Faculté des Sciences
Université Mohammed 1er, Oujda, Maroc
email: berrajaa@sciences.univ-oujda.ac.ma |
|---|
 |
Samir Lahrech
Département de Mathématiques et Informatique
Faculté des Sciences
Université Mohammed 1er, Oujda, Maroc
email: lahrech@sciences.univ-oujda.ac.ma |
|---|
Return to the table of contents for this conference.
Return to the EJDE web page
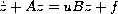 .
Viewing
.
Viewing
 as control,
we seek to minimize
as control,
we seek to minimize
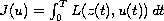 .
Under suitable hypotheses, it is shown that there exists an
optimal control
.
Under suitable hypotheses, it is shown that there exists an
optimal control
 and that it satisfies the
appropriate optimality system. An example involving the
and that it satisfies the
appropriate optimality system. An example involving the
 -Laplacian
operator demonstrates the applicability of our results.
-Laplacian
operator demonstrates the applicability of our results.


