2005-Oujda International Conference on Nonlinear Analysis,
Oujda, Morocco.
Electron. J. Diff. Eqns., Conference 14 (2006), pp. 95-107.
Maximum and anti-maximum principles for the p-Laplacian with a
nonlinear boundary condition
Aomar Anane, Omar Chakrone, Najat Moradi
Abstract:
In this paper we study the maximum and the anti-maximum principles
for the problem
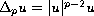 in the bounded smooth domain
in the bounded smooth domain
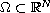 ,
with
,
with
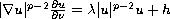 as a non linear boundary condition on
as a non linear boundary condition on
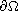 which
is supposed
which
is supposed
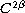 for some
for some
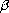 in
in
![$]0,1[$](gifs/ag.gif) ,
and where
,
and where
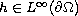 .
We will also examine the existence
and the non existence of the solutions and their signs.
.
We will also examine the existence
and the non existence of the solutions and their signs.
Published September 20, 2006.
Math Subject Classifications: 35J65, 35J25.
Key Words: Anti-maximum; p-laplacian; non linear boundary condition.
Show me the
PDF file (258K),
TEX file, and other files for this article.
 |
Aomar Anane
Département de Mathématiques et Informatique
Faculté des Sciences
Université Mohammed 1er, Oujda, Maroc
email: anane@sciences.univ-oujda.ac.ma |
 |
Omar Chakrone
Département de Mathématiques et Informatique
Faculté des Sciences
Université Mohammed 1er, Oujda, Maroc
email: chakrone@sciences.univ-oujda.ac.ma |
| |
Najat Moradi
Département de Mathématiques et Informatique
Faculté des Sciences
Université Mohammed 1er, Oujda, Maroc
email: najat_moradi@yahoo.fr |
|---|
Return to the table of contents for this conference.
Return to the EJDE web page
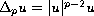 in the bounded smooth domain
in the bounded smooth domain
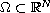 ,
with
,
with
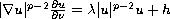 as a non linear boundary condition on
as a non linear boundary condition on
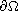 which
is supposed
which
is supposed
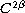 for some
for some
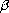 in
in
![$]0,1[$](gifs/ag.gif) ,
and where
,
and where
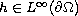 .
We will also examine the existence
and the non existence of the solutions and their signs.
.
We will also examine the existence
and the non existence of the solutions and their signs.

