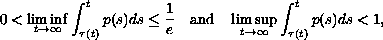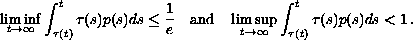2004 Conference on Diff. Eqns. and Appl. in Math. Biology, Nanaimo,
BC, Canada.
Electron. J. Diff. Eqns., Conference 12, 2005, pp. 171-180.
Oscillation criteria for functional differential equations
Ioannis P. Stavroulakis
Abstract:
Consider the first-order linear delay differential equation
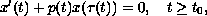
and the second-order linear delay equation
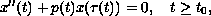
where
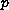 and
and
 are continuous functions on
are continuous functions on
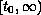 ,
,
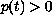 ,
,
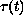 is non-decreasing,
is non-decreasing,
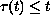 for
for
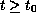 and
and
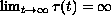 . Several oscillation
criteria are presented for the first-order equation when
. Several oscillation
criteria are presented for the first-order equation when
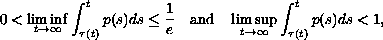
and for the second-order equation when
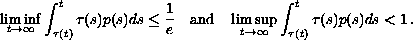
Published April 20, 2005.
Math Subject Classifications: 34K11, 34C10.
Key Words: Oscillation; delay differential equations.
Show me the
PDF file (236K),
TEX file, and other files for this article.
 |
Ioannis P. Stavroulakis
Department of Mathematics
University of Ioannina
451 10 Ioannina, Greece
email: ipstav@cc.uoi.gr |
|---|
Return to the EJDE web page
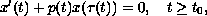
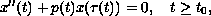
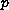 and
and
 are continuous functions on
are continuous functions on
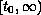 ,
,
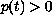 ,
,
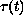 is non-decreasing,
is non-decreasing,
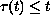 for
for
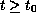 and
and
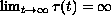 . Several oscillation
criteria are presented for the first-order equation when
. Several oscillation
criteria are presented for the first-order equation when