We obtain sufficient conditions for oscillation of solutions, and for asymptotical stability of the positive equilibrium, of the scalar nonlinear delay differential equation
![$$
\frac{dN}{dt} = r(t)N(t)\Big[a-\Big(\sum_{k=1}^m b_k N(g_k(t))
\Big)^{\gamma}\Big], $$](gifs/aa.gif)
where
.
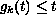Leonid Berezansky, Lev Idels
Abstract:
We obtain sufficient conditions for oscillation of solutions,
and for asymptotical stability of the positive equilibrium, of
the scalar nonlinear delay differential equation
where
.
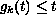Published April 20, 2005.
Math Subject Classifications: 34K11, 34K20, 34K60.
Key Words: Delay differential equations; Richard's nonlinearity;
oscillation; stability.
Show me the PDF file (206K), TEX file, and other files for this article.
 |
Leonid Berezansky Department of Mathematics Ben-Gurion University of the Negev Beer-Sheva 84105, Israel email: brznsky@cs.bgu.ac.il Phone 972-7-6461602 Fax 972-7-6281340 |
|---|---|
 |
Lev Idels Mathematics Department Malaspina University-College 900 Fifth Street Nanaimo, BC V9R 5S5, Canada email: lidels@shaw.ca Phone 250-753-3245 ext. 2429 Fax 250-740-6482 |
Return to the EJDE web page