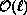 shift in Hopf bifurcations for a class of
non-standard numerical schemes.
shift in Hopf bifurcations for a class of
non-standard numerical schemes.
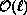 shift in Hopf bifurcations for a class of
non-standard numerical schemes.
shift in Hopf bifurcations for a class of
non-standard numerical schemes.
Murray E. Alexander, Seyed M. Moghadas
Abstract:
Quantitative aspects of models describing the dynamics of biological
phenomena have been mostly restricted to results of numerical
simulations, often by employing standard numerical methods. However,
several studies have shown that these methods may fail to reproduce
the actual dynamical behavior of the underlying continuous model
when the integration time-step, model parameters, or initial
conditions vary in their respective ranges. In this paper, a
non-standard numerical scheme is constructed for a general class of
positivity-preserving system of ordinary differential equations. A
connection between the dynamics of the system and that of the scheme
is established in terms of codimension-zero bifurcations. It is
shown that when the continuous model undergoes a bifurcation with a
simple eigenvalue passing through zero (pitchfork, transcritical or
saddle-node bifurcation), the scheme exhibits a corresponding
bifurcation at the same bifurcation parameter value. On the other
hand, for a Hopf bifurcation there is in general an
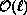 shift in the bifurcation parameter value for the
numerical scheme, where
shift in the bifurcation parameter value for the
numerical scheme, where
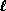 is the time-step. Partial results for
the bifurcations of codimension-1 and higher are also discussed.
Finally, the results are detailed for two examples: predator-prey
system of Gause-type and the Brusselator system representing an
autocatalytic oscillating chemical reaction.
is the time-step. Partial results for
the bifurcations of codimension-1 and higher are also discussed.
Finally, the results are detailed for two examples: predator-prey
system of Gause-type and the Brusselator system representing an
autocatalytic oscillating chemical reaction.
Published April 20, 2005.
Math Subject Classifications: 65P30, 65C20, 37M05.
Key Words: Finite-difference methods, Codimension-zero bifurcations,
Quantitative analysis, Scheme failure.
Show me the PDF file (568K), TEX file, and other files for this article.
| Murray E. Alexander Institute for Biodiagnostics National Research Council Canada Winnipeg, Manitoba, Canada R3B 1Y6 email: Murray.Alexander@nrc-cnrc.gc.ca | |
 |
Seyed M. Moghadas Institute for Biodiagnostics National Research Council Canada Winnipeg, Manitoba, Canada R3B 1Y6 email: Seyed.Moghadas@nrc-cnrc.gc.ca |
Return to the EJDE web page