2004-Fez conference on Differential Equations and Mechanics.
Electron. J. Diff. Eqns.,
Conference 11, 2004, pp. 81-93.
An infinite-harmonic analogue of a Lelong theorem
and infinite-harmonicity cells
Mohammed Boutaleb
Abstract:
We consider the problem of finding a function
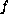 in
the set of
in
the set of
 -harmonic
functions, satisfying
-harmonic
functions, satisfying
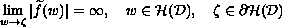
and being a solution to the quasi-linear parabolic equation
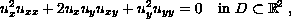
where
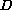 is a simply connected plane domain,
is a simply connected plane domain,
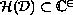 is the harmonicity cell of
is the harmonicity cell of
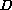 , and
, and
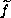 is the holomorphic extension of
is the holomorphic extension of
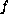 .
As an application, we show a
.
As an application, we show a
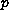 -harmonic
behaviour of the modulus of the
velocity of an arbitrary stationary plane flow near an extreme point of the
profile.
-harmonic
behaviour of the modulus of the
velocity of an arbitrary stationary plane flow near an extreme point of the
profile.
Published October 15, 2004.
Math Subject Classifications: 31A30, 31B30, 35J30.
Key Words: Infinite-harmonic functions; holomorphic extension;
harmonicity cells; p-Laplace equation; stationary plane flow.
Show me the
PDF file (304K),
TEX file, and other files for this article.
 |
Mohammed Boutaleb
Dép. de Mathématiques. Fac de
Sciences Fès D. M
B.P. 1796 Atlas Maroc
email: mboutalebmoh@yahoo.fr |
|---|
Return to the EJDE web page
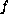 in
the set of
in
the set of
 -harmonic
functions, satisfying
-harmonic
functions, satisfying
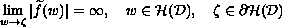
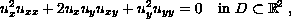
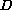 is a simply connected plane domain,
is a simply connected plane domain,
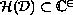 is the harmonicity cell of
is the harmonicity cell of
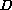 , and
, and
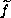 is the holomorphic extension of
is the holomorphic extension of
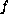 .
As an application, we show a
.
As an application, we show a
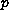 -harmonic
behaviour of the modulus of the
velocity of an arbitrary stationary plane flow near an extreme point of the
profile.
-harmonic
behaviour of the modulus of the
velocity of an arbitrary stationary plane flow near an extreme point of the
profile. 