2004-Fez conference on Differential Equations and Mechanics.
Electron. J. Diff. Eqns.,
Conference 11, 2004, pp. 61-70.
Doubly nonlinear parabolic equations related to the
p-Laplacian operator
Fatiha Benzekri, Abderrahmane El Hachimi
Abstract:
This paper concerns the doubly nonlinear parabolic P.D.E.
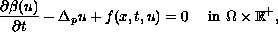
with Dirichlet boundary conditions and initial data.
We investigate here a time-discretization of the continuous
problem by the Euler forward scheme. In addition to
existence, uniqueness and stability questions, we study the
long-time behavior of the solution to the discrete problem.
We prove the existence of a global attractor, and obtain
regularity results under certain restrictions.
Published October 15, 2004.
Math Subject Classifications: 35K15, 35K60, 35J60.
Key Words: p-Laplacian; nonlinear parabolic equations;
semi-discretization; discrete dynamical system; attractor.
Show me the
PDF file (241K),
TEX file, and other files for this article.
 |
Fatiha Benzekri
UFR Mathématiques Appliquées et Industrielles
Faculté des sciences
B. P. 20, El Jadida, Maroc
email: benzekri@ucd.ac.ma
|
|---|
 |
Abderrahmane El Hachimi
UFR Mathématiques Appliquées et Industrielles
Faculté des Sciences
B.P. 20, El Jadida, Maroc
e-mail: elhachimi@ucd.ac.ma |
|---|
Return to the EJDE web page