We consider the eigenvalue wave equation
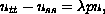
subject to
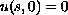 ,
where
,
where
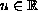 , is a function of
, is a function of
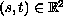 ,
with
,
with
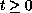 .
In the characteristic triangle
.
In the characteristic triangle
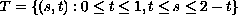 we impose a boundary condition along characteristics so that
we impose a boundary condition along characteristics so that

The parameters
 and
and
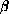 are arbitrary except for the condition that
they are not both zero. The two vectors
are arbitrary except for the condition that
they are not both zero. The two vectors
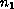 and
and
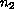 are the exterior unit normals
to the characteristic boundaries and
are the exterior unit normals
to the characteristic boundaries and
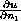 ,
,
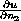 are the normal derivatives in those directions. When
are the normal derivatives in those directions. When
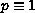 we will show that the above characteristic boundary value problem
has real, discrete eigenvalues and corresponding eigenfunctions
that are complete and orthogonal in
we will show that the above characteristic boundary value problem
has real, discrete eigenvalues and corresponding eigenfunctions
that are complete and orthogonal in
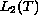 .
We will also investigate the case where
.
We will also investigate the case where
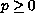 is an arbitrary continuous function in
is an arbitrary continuous function in
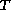 .
.
