Fifth Mississippi State Conference on Differential Equations and
Computational Simulations,
Electron. J. Diff. Eqns., Conf. 10, 2003, pp. 115-122.
Solutions series for some non-harmonic motion equations
A. Raouf Chouikha
Abstract:
We consider the class of nonlinear oscillators of the form
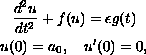
where
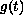 is a
is a
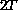 -periodic function,
-periodic function,
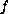 is a function only dependent on
is a function only dependent on
 , and
, and
 is a small parameter.
We are interested in the periodic solutions with minimal period
is a small parameter.
We are interested in the periodic solutions with minimal period
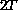 ,
when the restoring term
,
when the restoring term
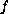 is such that
is such that
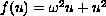 and
and
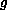 is a
trigonometric polynomial with period
is a
trigonometric polynomial with period
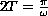 .
By using method based on expanding the solution as a sine power series,
we prove the existence of periodic solutions for this perturbed equation.
.
By using method based on expanding the solution as a sine power series,
we prove the existence of periodic solutions for this perturbed equation.
Published February 28, 2003.
Subject classifications: 34A20.
Key words: power series solution, trigonometric series.
Show me the
PDF file (178K),
TEX file, and other files for this article.
 |
A. Raouf Chouikha
University of Paris-Nord, Laga,
CNRS UMR 7539 Villetaneuse F-93430, France
e-mail: chouikha@math.univ-paris13.fr
|
Return to the table of contents
for this conference.
Return to the Electronic Journal of Differential Equations
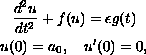
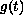 is a
is a
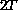 -periodic function,
-periodic function,
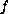 is a function only dependent on
is a function only dependent on
 , and
, and
 is a small parameter.
We are interested in the periodic solutions with minimal period
is a small parameter.
We are interested in the periodic solutions with minimal period
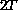 ,
when the restoring term
,
when the restoring term
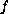 is such that
is such that
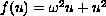 and
and
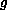 is a
trigonometric polynomial with period
is a
trigonometric polynomial with period
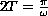 .
By using method based on expanding the solution as a sine power series,
we prove the existence of periodic solutions for this perturbed equation.
.
By using method based on expanding the solution as a sine power series,
we prove the existence of periodic solutions for this perturbed equation.
