Fifth Mississippi State Conference on Differential Equations and
Computational Simulations,
Electron. J. Diff. Eqns., Conf. 10, 2003, pp. 101-107.
A sign-changing solution for a superlinear Dirichlet problem, II
Alfonso Castro, Pavel Drabek, & John M. Neuberger
Abstract:
In previous work by Castro, Cossio, and Neuberger [2],
it was shown that a superlinear Dirichlet problem has
at least three nontrivial solutions when the derivative of the
nonlinearity at zero is less than the first eigenvalue of
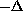 with zero Dirichlet boundry condition.
One of these solutions changes sign exactly-once and the other
two are of one sign.
In this paper we show that when this derivative is
between the k-th and k+1-st eigenvalues there still
exists a solution which changes sign at most k times.
In particular, when k=1 the sign-changing exactly-once
solution persists although one-sign solutions no longer exist.
with zero Dirichlet boundry condition.
One of these solutions changes sign exactly-once and the other
two are of one sign.
In this paper we show that when this derivative is
between the k-th and k+1-st eigenvalues there still
exists a solution which changes sign at most k times.
In particular, when k=1 the sign-changing exactly-once
solution persists although one-sign solutions no longer exist.
Published February 28, 2003.
Subject classifications: 35J20, 35J25, 35J60.
Key words: Dirichlet problem, superlinear, subcritical,
sign-changing solution, deformation lemma.
Show me the
PDF file (183K),
TEX file, and other files for this article.
 |
Alfonso Castro
Division of Mathematics and Statistics
University of Texas at San Antonio
San Antonio, TX 78249-0664, USA
e-mail: acastro@utsa.edu |
 |
Pavel Drabek
Department of Mathematics
University of West Bohemia
306 14 Pilsen, Czech Republic
e-mail address: pdrabek@kma.zcu.cz |
 |
John M. Neuberger
Department of Mathematics
Northern Arizona University
Flagstaff, AZ 86011-5717 USA
e-mail address: John.Neuberger@nau.edu |
Return to the table of contents
for this conference.
Return to the Electronic Journal of Differential Equations
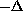 with zero Dirichlet boundry condition.
One of these solutions changes sign exactly-once and the other
two are of one sign.
In this paper we show that when this derivative is
between the k-th and k+1-st eigenvalues there still
exists a solution which changes sign at most k times.
In particular, when k=1 the sign-changing exactly-once
solution persists although one-sign solutions no longer exist.
with zero Dirichlet boundry condition.
One of these solutions changes sign exactly-once and the other
two are of one sign.
In this paper we show that when this derivative is
between the k-th and k+1-st eigenvalues there still
exists a solution which changes sign at most k times.
In particular, when k=1 the sign-changing exactly-once
solution persists although one-sign solutions no longer exist.


