Fifth Mississippi State Conference on Differential Equations and
Computational Simulations,
Electron. J. Diff. Eqns., Conf. 10, 2003, pp. 71-78.
Nonlinear initial-value problems with positive global solutions
John V. Baxley & Cynthia G. Enloe
Abstract:
We give conditions on
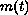 ,
,
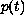 , and
, and
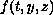 so that the nonlinear initial-value problem
so that the nonlinear initial-value problem
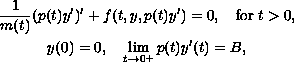
has at least one positive solution for all
 ,
when
,
when
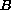 is a sufficiently small positive constant.
We allow a singularity at
is a sufficiently small positive constant.
We allow a singularity at
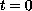 so the solution
so the solution
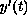 may be unbounded
near
may be unbounded
near
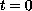 .
.
Published February 28, 2003.
Subject classifications: 34A12, 34B15.
Key words: Nonlinear initial-value problems, positive global solutions,
Caratheodory.
Show me the
PDF file (176K),
TEX file, and other files for this article.
 |
John V. Baxley
Department of Mathematics
Wake Forest University
Winston-Salem, NC 27109, USA
e-mail: baxley@mthcsc.wfu.edu |
 |
Cynthia G. Enloe
Department of Mathematics
Wake Forest University
Winston-Salem, NC 27109, USA |
Return to the table of contents
for this conference.
Return to the Electronic Journal of Differential Equations
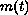 ,
,
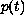 , and
, and
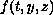 so that the nonlinear initial-value problem
so that the nonlinear initial-value problem
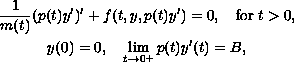
 ,
when
,
when
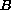 is a sufficiently small positive constant.
We allow a singularity at
is a sufficiently small positive constant.
We allow a singularity at
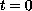 so the solution
so the solution
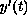 may be unbounded
near
may be unbounded
near
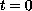 .
.

