Fifth Mississippi State Conference on Differential Equations and
Computational Simulations,
Electron. J. Diff. Eqns., Conf. 10, 2003, pp. 23-31.
An adaptive numerical method for the wave equation
with a nonlinear boundary condition
Azmy S. Ackleh, Keng Deng, & Joel Derouen
Abstract:
We develop an efficient numerical method for
studying the existence and non-existence of global solutions to the
initial-boundary value problem
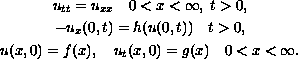
The results by this numerical method corroborate the theory presented in
[1]. Furthermore, they suggest that blow-up can occur for more general
nonlinearities
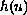 with weaker conditions on the initial data
with weaker conditions on the initial data
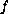 and
and
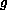 .
.
Published February 28, 2003.
Subject classifications: 35B40, 35L05, 35L20, 65M25, 65N50.
Key words: Time-adaptive numerical method, blow-up time, blow-up rate.
Show me the
PDF file (423K),
TEX file, and other files for this article.
 |
Azmy S. Ackleh
Department of Mathematics
University of Louisiana at Lafayette
Lafayette, Louisiana 70504, USA.
e-mail: ackleh@louisiana.edu
|
 |
Keng Deng
Department of Mathematics
University of Louisiana at Lafayette
Lafayette, Louisiana 70504, USA.
e-mail: deng@louisiana.edu
|
| |
Joel Derouen
Department of Mathematics
University of Louisiana at Lafayette
Lafayette, Louisiana 70504, USA.
e-mail: jbd8438@louisiana.edu
|
Return to the table of contents
for this conference.
Return to the Electronic Journal of Differential Equations
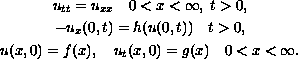
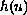 with weaker conditions on the initial data
with weaker conditions on the initial data
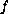 and
and
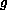 .
.

