2002-Fez conference on Partial Differental Equations,
Electron. J. Diff. Eqns., Conf. 09, 2002, pp. 149-160.
Local and global nonexistence of solutions to semilinear
evolution equations
Mohammed Guedda & Mokhtar Kirane
Abstract:
For a fixed
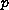 and
and
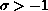 , such that
, such that
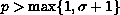 ,
one main concern of this paper is to find sufficient conditions
for non solvability of
,
one main concern of this paper is to find sufficient conditions
for non solvability of
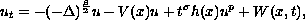
posed in
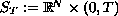 , where
, where
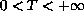 ,
,
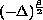 with
with
 is the
is the
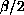 fractional power of the
fractional power of the
 , and
, and
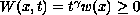 . The potential
. The potential
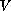 satisfies
satisfies
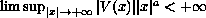 , for some
positive
, for some
positive
 .
We shall see that the existence of solutions depends on
the behavior at infinity of both initial data and the function
.
We shall see that the existence of solutions depends on
the behavior at infinity of both initial data and the function
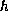 or of
both
or of
both
 and
and
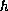 .
The non-global existence is also discussed. We
prove, among other things, that if
.
The non-global existence is also discussed. We
prove, among other things, that if
 satisfies
satisfies
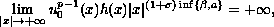
any possible local solution blows up at a finite time for any locally
integrable function
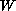 .
The situation is then extended to nonlinear
hyperbolic equations.
.
The situation is then extended to nonlinear
hyperbolic equations.
Published December 28, 2002.
Subject classfications: 35K55, 35K65, 35L60.
Key words: Parabolic inequality, hyperbolic equation,
fractional power, Fujita-type result.
Show me the
PDF file (227K),
TEX file, and other files for this article.
 |
Mohammed Guedda
Universite de Picardie Jules Verne
Faculte de Mathematiques et d'Informatique
33, rue Saint-Leu 80039 Amiens, France
e-mail: Guedda@u-picardie.fr |
|---|
 |
Mokthar Kirane
Laboratoire de Mathematiques,
Pole Sciences et Technologies,
Universite de la Rochelle,
Av. M. Crepeau,
17042 La Rochelle Cedex, France
e-mail: mokhtar.kirane@univ-lr.fr |
Return to the table of contents
for this conference.
Return to the Electronic Journal of Differential Equations
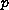 and
and
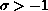 , such that
, such that
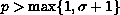 ,
one main concern of this paper is to find sufficient conditions
for non solvability of
,
one main concern of this paper is to find sufficient conditions
for non solvability of
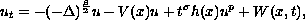
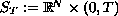 , where
, where
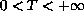 ,
,
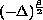 with
with
 is the
is the
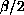 fractional power of the
fractional power of the
 , and
, and
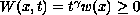 . The potential
. The potential
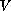 satisfies
satisfies
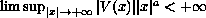 , for some
positive
, for some
positive
 .
We shall see that the existence of solutions depends on
the behavior at infinity of both initial data and the function
.
We shall see that the existence of solutions depends on
the behavior at infinity of both initial data and the function
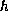 or of
both
or of
both
 and
and
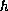 .
The non-global existence is also discussed. We
prove, among other things, that if
.
The non-global existence is also discussed. We
prove, among other things, that if
 satisfies
satisfies
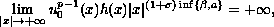
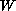 .
The situation is then extended to nonlinear
hyperbolic equations.
.
The situation is then extended to nonlinear
hyperbolic equations.

