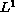 data
data
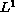 data
data
Elhoussine Azroul, Abdelmoujib Benkirane & Ouidad Filali
Abstract:
In this paper, we study the existence of solutions for strongly nonlinear
degenerated unilateral problems associated to nonlinear operators
of the form
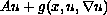 .
Here
.
Here
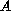 is a Leray-Lions operator
acting from
is a Leray-Lions operator
acting from
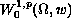 into its dual,
while
into its dual,
while
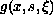 is a nonlinear term which has a growth condition
with respect to
is a nonlinear term which has a growth condition
with respect to
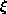 and no growth condition with respect to
and no growth condition with respect to
 ,
the second term belongs to
,
the second term belongs to
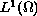 .
.
Published December 28, 2002.
Subject classfications: 35J15, 35J70, 35J85.
Key words: Weighted Sobolev spaces, Hardy inequality,
quasilinear degenerated elliptic operators.
Show me the PDF file (231K), TEX file, and other files for this article.
 |
Elhoussine Azroul Departement de Mathematiques et Informatique, Faculte des Sciences Dhar-Mahraz, B.P. 1796 Atlas, Fes, Maroc. e-mail: elazroul@caramail.com |
|---|---|
 |
Abdelmoujib Benkirane Departement de Mathematiques et Informatique, Faculte des Sciences Dhar-Mahraz, B.P. 1796 Atlas, Fes, Maroc. e-mail: abdelmoujib@iam.net.ma |
 |
Ouidad Filali Departement de Mathematiques et Informatique, Faculte des Sciences Dhar-Mahraz, B.P. 1796 Atlas, Fes, Maroc. e-mail: ouidadf@hotmail.com |
Return to the table of contents
for this conference.
Return to the Electronic Journal of Differential Equations