We shall prove an existence result of
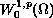 solutions for the
solutions for the
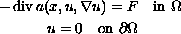
with right hand side in
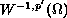 .
The features of the equation are that no
restrictions on the growth of the function
.
The features of the equation are that no
restrictions on the growth of the function
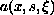 with
respect to
with
respect to
 are assumed and that
are assumed and that
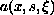 with respect to
with respect to
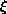 is monotone, but not strictly monotone. We overcome the
difficulty of the uncontrolled growth of
is monotone, but not strictly monotone. We overcome the
difficulty of the uncontrolled growth of
 thanks to a suitable
definition of solution (similar to the one introduced in [1]
for the study of the Dirichlet problem in
thanks to a suitable
definition of solution (similar to the one introduced in [1]
for the study of the Dirichlet problem in
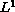 ) and the
difficulty of the not strict monotonicity thanks to a technique
(the
) and the
difficulty of the not strict monotonicity thanks to a technique
(the
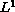 -version
of Minty's Lemma) similar to the one used in [5].
-version
of Minty's Lemma) similar to the one used in [5].
