USA-Chile Workshop on Nonlinear Analysis,
Electron. J. Diff. Eqns., Conf. 06, 2001, pp. 225-241.
Exponential dichotomies for linear systems with impulsive effects
Raul Naulin
Abstract:
In this paper we give conditions for the existence of a
dichotomy for the impulsive equation
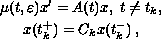
where
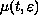 is a positive function such that
is a positive function such that
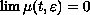 in some sense.
The results are expressed in terms of the properties of the
eigenvalues of matrices
in some sense.
The results are expressed in terms of the properties of the
eigenvalues of matrices
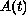 ,
the properties of the eigenvalues of matrices
,
the properties of the eigenvalues of matrices
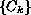 and the location of the impulsive times
and the location of the impulsive times
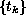 in
in
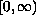 .
.
Published January 8, 2001.
Math Subject Classifications: 34A05, 34E05.
Key Words: Impulsive linear systems, singularly perturbed impulsive
systems, dichotomies, splitting of impulsive systems.
Show me the
PDF file (176K),
TEX file, and other files for this article.
Raul Naulin
Departamento de Matematicas,
Universidad de Oriente
Apartado 245, Cumana 6101-A, Venezuela
e-mail: rnaulin@cumana.sucre.udo.edu.ve
Return to the EJDE web page
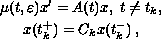
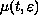 is a positive function such that
is a positive function such that
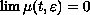 in some sense.
The results are expressed in terms of the properties of the
eigenvalues of matrices
in some sense.
The results are expressed in terms of the properties of the
eigenvalues of matrices
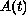 ,
the properties of the eigenvalues of matrices
,
the properties of the eigenvalues of matrices
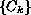 and the location of the impulsive times
and the location of the impulsive times
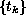 in
in
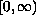 .
.