USA-Chile Workshop on Nonlinear Analysis,
Electron. J. Diff. Eqns., Conf. 06, 2001, pp. 173-187.
Behavior of positive radial solutions of a quasilinear equation
with a weighted Laplacian
Marta Garcia-Huidobro
Abstract:
We obtain a classification result for positive radially
symmetric solutions of the semilinear equation
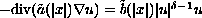 ,
,
on a punctured ball. The weight functions
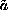 and
and
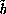 are
are
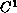 on the punctured ball, are positive and measurable almost everywhere,
and satisfy certain growth conditions near zero.
on the punctured ball, are positive and measurable almost everywhere,
and satisfy certain growth conditions near zero.
Published January 8, 2001.
Math Subject Classifications: 34B16.
Key Words: weighted Laplacian, singular solution, fundamental solution.
Show me the
PDF file (158K),
TEX file, and other files for this article.
 |
Marta Garcia-Huidobro
Departamento de Matematicas
Facultad de Matematica
Universidad Catolica de Chile
Casilla 306, Correo 22, Santiago, Chile
e-mail: mgarcia@poincare.mat.puc.cl |
Return to the EJDE web page
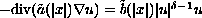 ,
,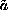 and
and
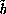 are
are
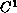 on the punctured ball, are positive and measurable almost everywhere,
and satisfy certain growth conditions near zero.
on the punctured ball, are positive and measurable almost everywhere,
and satisfy certain growth conditions near zero.
