USA-Chile Workshop on Nonlinear Analysis,
Electron. J. Diff. Eqns., Conf. 06, 2001, pp. 141-154.
Infinitely many solutions for an elliptic system with nonlinear
boundary conditions
Julian Fernandez Bonder, Juan Pablo Pinasco, & Julio D. Rossi
Abstract:
In this paper we prove the existence of infinitely many
nontrivial solutions of the system
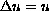 ,
,
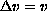 ,
,
with nonlinear coupling at the smooth boundary of a
bounded domain of
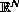 .
The proof, under suitable assumptions on the Hamiltonian, is based
on variational arguments and on the Fountain Theorem of the critical
.
The proof, under suitable assumptions on the Hamiltonian, is based
on variational arguments and on the Fountain Theorem of the critical
Published January 8, 2001.
Math Subject Classifications: 35J65, 35J50, 35J55.
Key Words: Elliptic systems, nonlinear boundary conditions,
variational problems.
Show me the
PDF file (165K),
TEX file, and other files for this article.
Julian Fernandez Bonder
Departamento de Matem\'atica, FCEyN
UBA (1428) Buenos Aires, Argentina
e-mail: jfbonder@dm.uba.ar
Juan Pablo Pinasco
Universidad de San Andres
Vito Dumas 284 (1684), Prov. Buenos Aires, Argentina
e-mail: jpinasco@udesa.edu.ar
Julio D. Rossi
Departamento de Matem\'atica, FCEyN
UBA (1428) Buenos Aires, Argentina
e-mail: jrossi@dm.uba.ar
Return to the EJDE web page
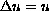 ,
,
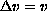 ,
,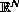 .
The proof, under suitable assumptions on the Hamiltonian, is based
on variational arguments and on the Fountain Theorem of the critical
.
The proof, under suitable assumptions on the Hamiltonian, is based
on variational arguments and on the Fountain Theorem of the critical