We study the existence of exponentially-bounded solutions to the following system of second-order ordinary differential equations with dissipation:
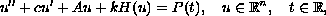
where
 and
and
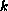 are positive constants,
are positive constants,
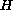 is a globally Lipschitz function, and
is a globally Lipschitz function, and
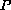 is a bounded and continuous function.
is a bounded and continuous function.
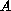 is a
is a
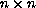 symmetric matrix whose first eigenvalue
is equal to zero and the others are positive.
Under these conditions, we prove that for some values of
symmetric matrix whose first eigenvalue
is equal to zero and the others are positive.
Under these conditions, we prove that for some values of
 ,
and
,
and
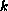 there exist a continuous manifold such that solutions starting
in this manifold are exponentially bounded.
Our results are applied to the spatial discretization of well-known
second-order partial differential equations with Neumann boundary
conditions.
there exist a continuous manifold such that solutions starting
in this manifold are exponentially bounded.
Our results are applied to the spatial discretization of well-known
second-order partial differential equations with Neumann boundary
conditions. 
