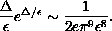Fourth Mississippi State Conference on
Differential Equations and Computational Simulations,
Electron. J. Diff. Eqns., Conf. 03, 1999, pp. 108-118.
On matched asymptotic analysis for laminar channel flow with
a turning point
Chunqing Lu
Abstract:
This paper presents a formal analysis of the asimptotic behaviour of
solutions of type III for the Berman equation

where
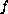 describes a laminar flow in a channel with porous walls.
A solution has a nonlinear turning point
describes a laminar flow in a channel with porous walls.
A solution has a nonlinear turning point
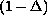 , i.e.\
, i.e.\
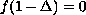 for some
for some
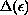 .
It is shown that
.
It is shown that
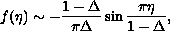
as
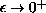 ,
for
,
for
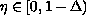 where
where
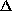 satisfies
satisfies
Published July 10, 2000.
Math Subject Classifications: 34B15, 34E05, 34E20.
Key Words: singular perturbations, turning point, laminar flow,
transcendental terms.
Show me the
PDF file (137K),
TEX file, and other files for this article.
Department of Mathematics and Statistics
Southern Illinois University at Edwardsville
Edwardsville, IL 62026 USA
e-mail: clu@siue.edu
Return to the EJDE web page

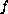 describes a laminar flow in a channel with porous walls.
A solution has a nonlinear turning point
describes a laminar flow in a channel with porous walls.
A solution has a nonlinear turning point
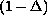 , i.e.\
, i.e.\
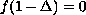 for some
for some
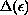 .
It is shown that
.
It is shown that
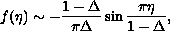
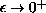 ,
for
,
for
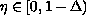 where
where
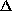 satisfies
satisfies