Fourth Mississippi State Conference on
Differential Equations and Computational Simulations,
Electron. J. Diff. Eqns., Conf. 03, 1999, pp. 75-90.
A singular nonlinear boundary-value problem
Robert M. Houck & Stephen B. Robinson
Abstract:
In this paper we prove an existence and uniqueness theorem for the
singular nonlinear boundary-value problem
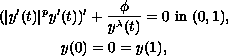
where
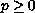 ,
,
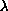 is a positive constant, and
is a positive constant, and
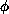 is a positive function in
is a positive function in
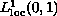 .
Moreover, we derive asymptotic estimates describing the
behavior of the solution and its derivative at the boundary.
.
Moreover, we derive asymptotic estimates describing the
behavior of the solution and its derivative at the boundary.
Published July 10, 2000.
Math Subject Classifications: 34B15.
Key Words: Singular nonlinear boundary value problems,
existence and uniqueness, asymptotic estimates.
Show me the
PDF file (174K),
TEX file, and other files for this article.
Robert M. Houck
Department of Mathematics and Computer Science
Wake Forest University
Winston-Salem, NC 27109, USA
e-mail: houck@mthcsc.wfu.edu
Stephen B. Robinson
Department of Mathematics and Computer Science
Wake Forest University
Winston-Salem, NC 27109, USA
e-mail: robinson@mthcsc.wfu.edu
Return to the EJDE web page
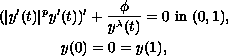
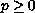 ,
,
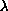 is a positive constant, and
is a positive constant, and
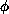 is a positive function in
is a positive function in
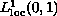 .
Moreover, we derive asymptotic estimates describing the
behavior of the solution and its derivative at the boundary.
.
Moreover, we derive asymptotic estimates describing the
behavior of the solution and its derivative at the boundary.