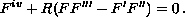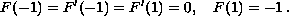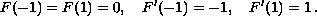Differential Equations and Computational Simulations III
Electron. J. Diff. Eqns., Conf. 01, 1997, pp. 159-170.
On the existence of steady flow in a channel with one porous wall
or two accelerating walls
Chunqing Lu
Abstract:
This paper presents a rigorous proof of the existence of steady flows in a
channel either with no-slip at one wall and constant uniform suction or
injection through another wall, or with two accelerating walls.
The flows are governed by the fourth order nonlinear differential equation
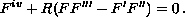
In the former case, the flow is subject to the boundary conditions
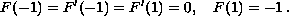
In the latter case, the boundary conditions are
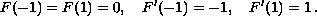
Published November 12, 1998.
Mathematics Subject Classifications: 34B15, 76D05.
Key words and phrases: laminar flow, similarity solutions, Navier-Stokes
equations.
Show me the
PDF file (152K),
TEX file, and other files for this article.
Chunqing Lu
Department of Mathematics and Statistics
Southern Illinois University at Edwardsville
Edwardsville, Illinois 62026, USA
Email address: clu@siue.edu
Return to the Proceedings of Conferences:
Electr. J. Diff. Eqns.