Differential Equations and Computational Simulations III
Electron. J. Diff. Eqns., Conf. 01, 1997, pp. 1-9.
Holder solutions for the amorphous silicon system and related problems
Walter Allegretto, Yanping Lin, & Aihui Zhou
Abstract:
We present existence of solutins and other results for the partial
differential equation system with memory which models
amorphous silicon devices and related problems in
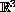 .
Our approach employs only classical estimates and
Degree Theory; it shows the existence of
.
Our approach employs only classical estimates and
Degree Theory; it shows the existence of
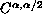 solutions for some
solutions for some
 . In view
of the mixed boundary conditions, this is the maximum
regularity that can be expected.
. In view
of the mixed boundary conditions, this is the maximum
regularity that can be expected.
Published November 12, 1998.
Mathematics Subject Classifications: 35J60.
Key words: Reaction, diffusion, semiconductor, Holder continuous solutions.
Show me the
PDF file (141K),
TEX file, and other files for this article.
 |
Walter Allegretto
Department of Mathematical Sciences
University of Alberta
Edmonton, Alberta, Canada T6G 2G1
Email address: retl@retl.math.ualberta.ca |
 |
Yanping Lin
Department of Mathematical Sciences
University of Alberta
Edmonton, Alberta, Canada T6G 2G1
Email address: ylin@hilbert.math.ualberta.ca |
 |
Aihui Zhou
Institute of Systems Science, Academia Sinica
Beijing 100080, China
Email address: azhou@bamboo.iss.ac.cn |
Return to the Proceedings of Conferences:
Electr. J. Diff. Eqns.
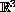 .
Our approach employs only classical estimates and
Degree Theory; it shows the existence of
.
Our approach employs only classical estimates and
Degree Theory; it shows the existence of
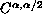 solutions for some
solutions for some
 . In view
of the mixed boundary conditions, this is the maximum
regularity that can be expected.
. In view
of the mixed boundary conditions, this is the maximum
regularity that can be expected.


