Electron. J. Differential Equations,
Vol. 2019 (2019), No. 13, pp. 1-16.
Existence of infinitely many small solutions for sublinear fractional
Kirchhoff-Schrodinger-Poisson systems
Jose Carlos de Albuquerque, Rodrigo Clemente, Diego Ferraz
Abstract:
We study the Kirchhoff-Schrodinger-Poisson system
![$$\displaylines{
m([u]_{\alpha}^2)(-\Delta)^\alpha u+V(x)u+k(x)\phi u = f(x,u), \quad
x\in\mathbb{R}^3,\cr
(-\Delta)^\beta \phi = k(x)u^2, \quad x\in\mathbb{R}^3,
}$$](images/aa.png)
where
![$[\cdot]_{\alpha}$](images/ab.png) denotes the Gagliardo semi-norm,
denotes the Gagliardo semi-norm,
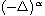 denotes the fractional Laplacian operator with
denotes the fractional Laplacian operator with
![$\alpha,\beta\in (0,1]$](images/ad.png) ,
,
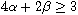 and
and
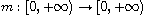 is a Kirchhoff function satisfying
suitable assumptions. The functions V(x) and k(x) are nonnegative and
the nonlinear term f(x,s) satisfies certain local conditions.
By using a variational approach, we use a Kajikiya's version of the
symmetric mountain pass lemma and Moser iteration method to prove the
existence of infinitely many small solutions.
is a Kirchhoff function satisfying
suitable assumptions. The functions V(x) and k(x) are nonnegative and
the nonlinear term f(x,s) satisfies certain local conditions.
By using a variational approach, we use a Kajikiya's version of the
symmetric mountain pass lemma and Moser iteration method to prove the
existence of infinitely many small solutions.
Submitted June 25, 2018. Published January 25, 2019.
Math Subject Classifications: 35A15, 35J50, 35R11, 45G05.
Key Words: Kirchhoff-Schrodinger-Poisson equation; fractional Laplacian;
variational method.
Show me the PDF file (306 KB),
TEX file for this article.
 |
José Carlos de Albuquerque
Institute of Mathematics and Statistics
Federal University of Goiás
74001-970, Goiânia, Goiás, Brazil
email: joserre@gmail.com
|
|---|
 |
Rodrigo Clemente
Department of Mathematics
Rural Federal University of Pernambuco
52171-900, Recife, Pernambuco, Brazil
email: rodrigo.clemente@ufrpe.br
|
|---|
 |
Diego Ferraz
Department of Mathematics
Federal University of Rio Grande do Norte
59078-970, Natal, Rio Grande do Norte, Brazil
email: diego.ferraz.br@gmail.com
|
|---|
Return to the EJDE web page
![$$\displaylines{
m([u]_{\alpha}^2)(-\Delta)^\alpha u+V(x)u+k(x)\phi u = f(x,u), \quad
x\in\mathbb{R}^3,\cr
(-\Delta)^\beta \phi = k(x)u^2, \quad x\in\mathbb{R}^3,
}$$](images/aa.png)
![$[\cdot]_{\alpha}$](images/ab.png) denotes the Gagliardo semi-norm,
denotes the Gagliardo semi-norm,
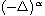 denotes the fractional Laplacian operator with
denotes the fractional Laplacian operator with
![$\alpha,\beta\in (0,1]$](images/ad.png) ,
,
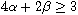 and
and
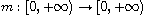 is a Kirchhoff function satisfying
suitable assumptions. The functions V(x) and k(x) are nonnegative and
the nonlinear term f(x,s) satisfies certain local conditions.
By using a variational approach, we use a Kajikiya's version of the
symmetric mountain pass lemma and Moser iteration method to prove the
existence of infinitely many small solutions.
is a Kirchhoff function satisfying
suitable assumptions. The functions V(x) and k(x) are nonnegative and
the nonlinear term f(x,s) satisfies certain local conditions.
By using a variational approach, we use a Kajikiya's version of the
symmetric mountain pass lemma and Moser iteration method to prove the
existence of infinitely many small solutions.


