Electron. J. Differential Equations,
Vol. 2019 (2019), No. 06, pp. 1-30.
Competitive exclusion in a multi-strain SIS epidemic model
on complex networks
Junyuan Yang, Toshikazu Kuniya, Xiaofeng Lu
Abstract:
In this article, we propose an infection age-structured multi-strain
SIS epidemic model on complex networks. We obtain the reproduction
numbers for each strain by using the classical theory of renewal equations,
and we define the basic reproduction number
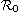 for the whole
system by the maximum of them. We prove that if
for the whole
system by the maximum of them. We prove that if
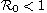 ,
then the disease-free equilibrium of the model is globally asymptotically
stable, whereas if
,
then the disease-free equilibrium of the model is globally asymptotically
stable, whereas if
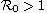 ,
then there exists an endemic
equilibrium in which only one strain with the largest reproduction number
survives. Moreover, under an additional assumption that the recovery rate
is homogeneous, we prove that such an endemic equilibrium is globally
asymptotically stable. Interestingly, our theoretical results imply that
the competitive exclusion can occur in a sense that only one strain with
the largest reproduction number survives.
,
then there exists an endemic
equilibrium in which only one strain with the largest reproduction number
survives. Moreover, under an additional assumption that the recovery rate
is homogeneous, we prove that such an endemic equilibrium is globally
asymptotically stable. Interestingly, our theoretical results imply that
the competitive exclusion can occur in a sense that only one strain with
the largest reproduction number survives.
Submitted May 17, 2018. Published January 14, 2019.
Math Subject Classifications: 35Q92, 35R02, 37N25, 92D30.
Key Words: Multi-strain SIS epidemic model; complex network;
infection age; basic reproduction number; global stability;
competitive exclusion.
Show me the PDF file (1359 KB),
TEX file for this article.
 |
Junyuan Yang
Complex Systems Research Center
Shanxi University
Taiyuan 030006, Shanxi, China
email: yangjunyuan00@126.com
|
|---|
 |
Toshikazu Kuniya
Graduate School of System Informatics
Kobe University, 1-1 Rokkodai-cho
Nada-ku, Kobe 657-8501, Japan
email: tkuniya@port.kobe-u.ac.jp
|
|---|
 |
Xiaofeng Luo
Complex Systems Research Center
Shanxi University
Taiyuan 030006, Shanxi, China
email: luo_xf1988@163.com
|
|---|
Return to the EJDE web page
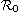 for the whole
system by the maximum of them. We prove that if
for the whole
system by the maximum of them. We prove that if
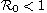 ,
then the disease-free equilibrium of the model is globally asymptotically
stable, whereas if
,
then the disease-free equilibrium of the model is globally asymptotically
stable, whereas if
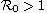 ,
then there exists an endemic
equilibrium in which only one strain with the largest reproduction number
survives. Moreover, under an additional assumption that the recovery rate
is homogeneous, we prove that such an endemic equilibrium is globally
asymptotically stable. Interestingly, our theoretical results imply that
the competitive exclusion can occur in a sense that only one strain with
the largest reproduction number survives.
,
then there exists an endemic
equilibrium in which only one strain with the largest reproduction number
survives. Moreover, under an additional assumption that the recovery rate
is homogeneous, we prove that such an endemic equilibrium is globally
asymptotically stable. Interestingly, our theoretical results imply that
the competitive exclusion can occur in a sense that only one strain with
the largest reproduction number survives.


