In this article we study a non-self-adjoint eigenparameter dependent singular differential 1D Hamiltonian system with the singular end points a and b in the Hilbert space
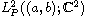and we consider
that this 1D Hamiltonian system is in the limit-circle cases at a and b.
For this purpose we use the maximal dissipative operator associated with
the considered problem whose spectral analysis is sufficient for boundary
value problem. Self-adjoint dilation theory of Sz.-Nagy-Foias developed
for the dissipative operators is used. Moreover we construct incoming and
outgoing spectral representations of the self-adjoint dilation.
This representations allows us to determine the scattering matrix.
Therefore a functional model of the dissipative operator is constructed.
Moreover, a functional model of the dissipative operator is constructed and
its characteristic function in terms of solutions of the corresponding
Hamiltonian system is described. Therefore using the obtained results for
the characteristic function theory, theorems on completeness of the system
of eigenvectors and associated vectors of the dissipative operator and
Hamiltonian boundary value problem have been proved.
