Electron. J. Differential Equations,
Vol. 2019 (2019), No. 01, pp. 1-11.
Integrability of very weak solution to the Dirichlet problem of nonlinear
elliptic system
Yuxia Tong, Shuang Liang, Shenzhou Zheng
Abstract:
This article concerns the higher integrability of a very weak solution
 for
for
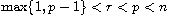 to the
Dirichlet problem of the nonlinear elliptic system
to the
Dirichlet problem of the nonlinear elliptic system
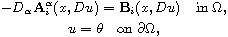
where
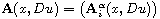 for
for
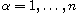 and
and
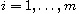 ,
and each entry of
,
and each entry of
 for
for
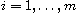 satisfies the monotonicity and controllable growth. If
satisfies the monotonicity and controllable growth. If
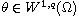 for q>r, then we derive that the very weak solution u of above-mentioned
problem is integrable with
for q>r, then we derive that the very weak solution u of above-mentioned
problem is integrable with
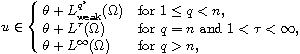
provided that r is sufficiently close to p, where
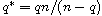 .
.
Submitted December 16, 2017. Published January 2, 2019.
Math Subject Classifications: 35D30, 35K10.
Key Words: Integrability; very weak solution; nonlinear elliptic system;
controllable growth.
Show me the PDF file (246 KB),
TEX file for this article.
 |
Yuxia Tong
Department of Mathematics
Beijing Jiaotong University
Beijing 100044, China
email: tongyuxia@bjtu.edu.cn
|
|---|
 |
Shuang Liang
Department of Mathematics
Beijing Jiaotong University
Beijing 100044, China
email: shuangliang@bjtu.edu.cn
|
|---|
 |
Shenzhou Zheng
Department of Mathematics
Beijing Jiaotong University
Beijing 100044, China
email: shzhzheng@bjtu.edu.cn
|
|---|
Return to the EJDE web page
 for
for
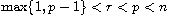 to the
Dirichlet problem of the nonlinear elliptic system
to the
Dirichlet problem of the nonlinear elliptic system
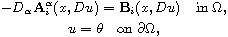
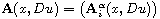 for
for
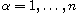 and
and
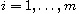 ,
and each entry of
,
and each entry of
 for
for
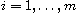 satisfies the monotonicity and controllable growth. If
satisfies the monotonicity and controllable growth. If
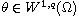 for q>r, then we derive that the very weak solution u of above-mentioned
problem is integrable with
for q>r, then we derive that the very weak solution u of above-mentioned
problem is integrable with
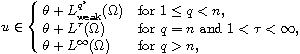
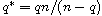 .
.


