Electron. J. Differential Equations,
Vol. 2018 (2018), No. 97, pp. 1-13.
Infinitely many solutions for sublinear fractional Schrodinger-type
equations with general potentials
Gang-Ling Hou, Bin Ge, Jian-Fang Lu
Abstract:
This article concerns the fractional Schrodinger type equations

where
 ,
,
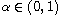 ,
,
 stands for the
fractional Laplacian,
stands for the
fractional Laplacian,
 is a positive continuous potential,
is a positive continuous potential,
 .
We establish criteria that guarantee the existence of infinitely many
solutions by using the genus properties in critical point theory.
.
We establish criteria that guarantee the existence of infinitely many
solutions by using the genus properties in critical point theory.
Submitted January 27, 2018. Published April 24, 2018.
Math Subject Classifications: 26A33, 35J60, 47J30.
Key Words: Fractional Laplacian; variational method; sublinear; genus.
Show me the PDF file (255 KB),
TEX file for this article.
 |
Gang-Ling Hou
College of Aerospace and Civil Engineering
Harbin Engineering University
Harbin, 150001, China
email: hougl@hrbeu.edu.cn
|
|---|
 |
Bin Ge
Department of Applied Mathematics
Harbin Engineering University
Harbin, 150001, China
email: gebin791025@hrbeu.edu.cn
|
|---|
 |
Jian-Fang Lu
Department of Applied Mathematics
Harbin Engineering University
Harbin, 150001, China
email: 1176678630@qq.com
|
|---|
Return to the EJDE web page

 ,
,
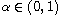 ,
,
 stands for the
fractional Laplacian,
stands for the
fractional Laplacian,
 is a positive continuous potential,
is a positive continuous potential,
 .
We establish criteria that guarantee the existence of infinitely many
solutions by using the genus properties in critical point theory.
.
We establish criteria that guarantee the existence of infinitely many
solutions by using the genus properties in critical point theory.


