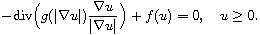Electron. J. Differential Equations, Vol. 2018 (2018), No. 91, pp. 1-9.

Harnack inequality for quasilinear elliptic equations with (p,q) growth conditions and absorption lower order term

Kateryna Buryachenko

Abstract:
In this article we study the quasilinear elliptic equation with absorption lower term
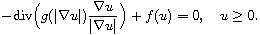
$$ -\hbox{div} \Big(g(|\nabla u|)\frac{\nabla u}{|\nabla u|}\Big)+f(u)= 0, \quad u\geq 0. $$
Despite of the lack of comparison principle, we prove a priori estimate of Keller-Osserman type. Particularly, under some natural assumptions on the functions g,f for nonnegative solutions we prove an estimate of the form
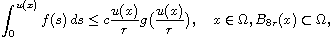
$$ \int_0^{u(x)} f(s)\,ds\leq c\frac{u(x)}{r}g\big(\frac{u(x)}{r}\big),\quad x\in\Omega, B_{8r}(x)\subset\Omega, $$
with constant c, independent on u(x). Using this estimate we give a simple proof of the Harnack inequality.

Submitted June 14, 2017. Published April 16, 2018.
Math Subject Classifications: 35J15, 35J60, 35J62.
Key Words: Harnack inequality; quasilinear elliptic equation; Keller-Osserman type estimate; absorption lower term.

Show me the PDF file (247 KB), TEX file for this article.

Kateryna Buryachenko
Vasyl' Stus Donetsk National University
600-richa Str., 21
Vinnytsia, 21021, Ukraine
email: katarzyna_@ukr.net

Return to the EJDE web page