Electron. J. Differential Equations,
Vol. 2018 (2018), No. 89, pp. 1-10.
p-Kirchhoff type problem with a general critical nonlinearity
Huixing Zhang, Baiquan Lin
Abstract:
In this article, we consider the p-Kirchhoff type problem
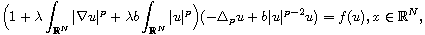
where
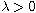 ,
the nonlinearity f can reach critical growth.
Without the Ambrosetti-Robinowitz condition or the monotonicity condition
on f, we prove the existence of positive solutions for the p-Kirchhoff
type problem. In addition, we also study the asymptotic behavior of the
solutions with respect to the parameter
,
the nonlinearity f can reach critical growth.
Without the Ambrosetti-Robinowitz condition or the monotonicity condition
on f, we prove the existence of positive solutions for the p-Kirchhoff
type problem. In addition, we also study the asymptotic behavior of the
solutions with respect to the parameter
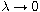 .
.
Submitted September 5, 2017. Published April 11, 2018.
Math Subject Classifications: 35B25, 35B33, 35J61.
Key Words: p-Kirchhoff type problem; critical growth; variational methods.
Show me the PDF file (245 KB),
TEX file for this article.
 |
Huixing Zhang
School of Mathematics and
School of Safety Engineering
China University of Mining and Technology
Xuzhou, Jiangsu 221116, China
email: huixingzhangcumt@163.com
|
|---|
| |
Baiquan Lin
School of Safety Engineering
China University of Mining and Technology
Xuzhou, Jiangsu 221116, China
email: lbq21405@126.com
|
|---|
Return to the EJDE web page
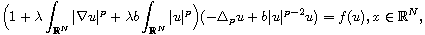
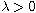 ,
the nonlinearity f can reach critical growth.
Without the Ambrosetti-Robinowitz condition or the monotonicity condition
on f, we prove the existence of positive solutions for the p-Kirchhoff
type problem. In addition, we also study the asymptotic behavior of the
solutions with respect to the parameter
,
the nonlinearity f can reach critical growth.
Without the Ambrosetti-Robinowitz condition or the monotonicity condition
on f, we prove the existence of positive solutions for the p-Kirchhoff
type problem. In addition, we also study the asymptotic behavior of the
solutions with respect to the parameter
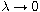 .
.
