Electron. J. Differential Equations,
Vol. 2018 (2018), No. 81, pp. 1-11.
Liouville-type theorems for stable solutions of singular
quasilinear elliptic equations in R^N
Caisheng Chen, Hongxue Song, Hongwei Yang
Abstract:
We prove a Liouville-type theorem for stable solution of the singular
quasilinear elliptic equations
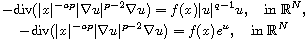
where
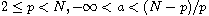 and the function f(x) is continuous
and nonnegative in
and the function f(x) is continuous
and nonnegative in
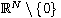 such that
such that
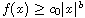 as
as
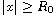 ,
with
,
with
 and
and
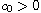 .
The results hold for
.
The results hold for
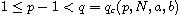 in the first equation,
and for
in the first equation,
and for
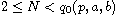 in the second equation.
Here
in the second equation.
Here
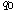 and
and
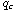 are exponents, which are always larger than the
classical critical ones and depend on the parameters a,b.
are exponents, which are always larger than the
classical critical ones and depend on the parameters a,b.
Submitted June 26, 2017. Published March 22, 2018.
Math Subject Classifications: 35J60, 35B53, 35B33, 35B45.
Key Words: Singular quasilinear elliptic equation; stable solutions;
critical exponents; Liouville type theorems.
Show me the PDF file (261 KB),
TEX file for this article.
 |
Caisheng Chen
College of Science, Hohai University
Nanjing 210098, China
email: cshengchen@hhu.edu.cn
|
|---|
 |
Hongxue Song
College of Science, Hohai University
Nanjing 210098, China
email: songhx@njupt.edu.cn
|
|---|
 |
Hongwei Yang
College of Mathematics and System Science
Shandong University of Science and Technology
Qingdao 266590, China
email: hwyang1979@163.com
|
|---|
Return to the EJDE web page
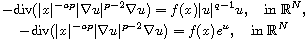
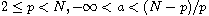 and the function f(x) is continuous
and nonnegative in
and the function f(x) is continuous
and nonnegative in
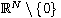 such that
such that
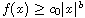 as
as
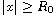 ,
with
,
with
 and
and
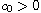 .
The results hold for
.
The results hold for
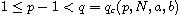 in the first equation,
and for
in the first equation,
and for
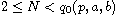 in the second equation.
Here
in the second equation.
Here
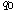 and
and
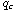 are exponents, which are always larger than the
classical critical ones and depend on the parameters a,b.
are exponents, which are always larger than the
classical critical ones and depend on the parameters a,b.


