Let
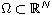 be a smooth bounded domain and let
a,b,c be three (possibly discontinuous and unbounded) T-periodic functions
with
be a smooth bounded domain and let
a,b,c be three (possibly discontinuous and unbounded) T-periodic functions
with
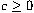 . We study existence and nonexistence of positive solutions for
periodic parabolic problems
. We study existence and nonexistence of positive solutions for
periodic parabolic problems
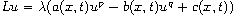 in
in
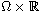 with Dirichlet boundary condition, where
with Dirichlet boundary condition, where
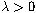 is a real parameter and
is a real parameter and
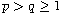 .
If a and b satisfy some additional conditions and
.
If a and b satisfy some additional conditions and
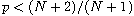 multiplicity results are also given. Qualitative properties of the
solutions are discussed as well. Our approach relies on the sub and
supersolution method (both to find
the stable solution as well as the unstable one) combined with some facts
about linear problems with indefinite weight.
All results remain true for the corresponding elliptic problems.
Moreover, in this case the growth restriction becomes
multiplicity results are also given. Qualitative properties of the
solutions are discussed as well. Our approach relies on the sub and
supersolution method (both to find
the stable solution as well as the unstable one) combined with some facts
about linear problems with indefinite weight.
All results remain true for the corresponding elliptic problems.
Moreover, in this case the growth restriction becomes
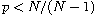 .
.

