We investigate the critical period bifurcations of the system
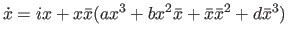
studied in [6]. We prove that at most three critical periods can bifurcate from any nonlinear center of the system.
Valery G. Romanovski, Maoan Han, Wentao Huang
Abstract:
We investigate the critical period bifurcations of the system
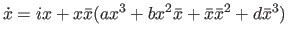
studied in [6]. We prove that at most three critical periods
can bifurcate from any nonlinear center of the system.
Submitted March 17, 2017. Published March 13, 2018.
Math Subject Classifications: 34C23, 34C25, 37G15.
Key Words: Critical period; bifurcation; isochronicity; polynomial systems.
Show me the PDF file (341 KB), TEX file for this article.
 |
Valery G. Romanovski Department of Mathematics Shanghai Normal University Shanghai 200234, China email: valery.romanovsky@uni-mb.si |
|---|---|
 |
Maoan Han Department of Mathematics Shanghai Normal University Shanghai 200234, China email: mahan@shnu.edu.cn |
 |
Wentao Huang School of Science Guilin University of Aerospace Technology Guilin, 541004, China email: huangwentao@163.com |
Return to the EJDE web page