Electron. J. Differential Equations,
Vol. 2018 (2018), No. 60, pp. 1-32.
Critical second-order elliptic equation with
zero Dirichlet boundary condition in four dimensions
Zakaria Boucheche, Hichem Chtioui, Hichem Hajaiej
Abstract:
We are concerned with the nonlinear critical problem
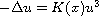 ,
,
 in
in
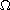 ,
,
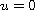 on
on
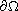 ,
where
,
where
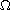 is a bounded domain of
is a bounded domain of
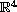 .
Under the
assumption that
.
Under the
assumption that
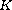 is strictly decreasing in the outward normal
direction on
is strictly decreasing in the outward normal
direction on
 and degenerate at its critical points
for an order
and degenerate at its critical points
for an order
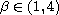 ,
we provide a complete
description of the lack of compactness of the associated variational
problem and we prove an existence result of Bahri-Coron type.
,
we provide a complete
description of the lack of compactness of the associated variational
problem and we prove an existence result of Bahri-Coron type.
Submitted October 22, 2017. Published March 2, 2018.
Math Subject Classifications: 35J60, 58E30.
Key Words: Elliptic equation; critical Sobolev exponent; variational method;
critical point at infinity.
Show me the PDF file (403 KB),
TEX file for this article.
Zakaria Boucheche
Department of mathematics
Faculty of Sciences of Sfax
3018 Sfax, Tunisia
email: Zakaria.Boucheche@ipeim.rnu.tn
|
Hichem Chtioui
Department of mathematics
Faculty of Sciences of Sfax
3018 Sfax, Tunisia
email: Hichem.Chtioui@fss.rnu.tn
|
Hichem Hajaiej
California State University Los Angeles
5151 University Drive
Los Angeles, CA 90032, USA
email: hichem.hajaiej@gmail.com
|
Return to the EJDE web page
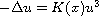 ,
,
 in
in
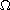 ,
,
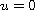 on
on
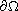 ,
where
,
where
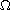 is a bounded domain of
is a bounded domain of
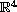 .
Under the
assumption that
.
Under the
assumption that
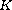 is strictly decreasing in the outward normal
direction on
is strictly decreasing in the outward normal
direction on
 and degenerate at its critical points
for an order
and degenerate at its critical points
for an order
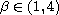 ,
we provide a complete
description of the lack of compactness of the associated variational
problem and we prove an existence result of Bahri-Coron type.
,
we provide a complete
description of the lack of compactness of the associated variational
problem and we prove an existence result of Bahri-Coron type.