Electron. J. Differential Equations,
Vol. 2018 (2018), No. 53, pp. 1-6.
Almost entire solutions of the Burgers equation
Nicholas D. Alikakos, Dimitrios Gazoulis
Abstract:
We consider Burgers equation on the whole x-t plane.
We require the solution to be classical everywhere, except possibly
over a closed set S of potential singularities, which is
(a) a subset of a countable union of ordered graphs of differentiable
functions,
(b) has one dimensional Hausdorff measure,
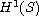 , equal to zero.
, equal to zero.
We establish that under these conditions the solution is identically equal
to a constant.
Submitted November 21, 2016. Published February 20, 2018.
Math Subject Classifications: 35B08, 35L65.
Key Words: Burgers equation; entropy solution; rigidity.
Show me the PDF file (180 KB),
TEX file for this article.
Nicholas D. Alikakos
Department of Mathematics,
University of Athens
panepistimioupolis 15784 Athens, Greece
email: nalikako@math.uoa.gr
|
Dimitrios Gazoulis
Department of Mathematics,
University of Athens
panepistimioupolis 15784 Athens, Greece
email: dgazoulis@math.uoa.gr
|
Return to the EJDE web page
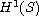 , equal to zero.
, equal to zero.