Electron. J. Differential Equations,
Vol. 2018 (2018), No. 41, pp. 1-10.
Ambrosetti-Prodi problem with degenerate potential and Neumann
boundary condition
Dusan D. Repovs
Abstract:
We study the degenerate elliptic equation
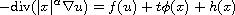
in a bounded open set
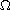 with homogeneous Neumann boundary
condition, where
with homogeneous Neumann boundary
condition, where
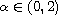 and f has a linear growth.
The main result establishes the existence of real numbers
and f has a linear growth.
The main result establishes the existence of real numbers
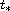 and
and
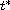 such that the problem has at least two solutions if
such that the problem has at least two solutions if
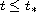 ,
there is
at least one solution if
,
there is
at least one solution if
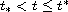 ,
and no solution exists
for all
,
and no solution exists
for all
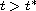 .
The proof combines a priori estimates with
topological degree arguments.
.
The proof combines a priori estimates with
topological degree arguments.
Submitted July 20, 2017. Published February 6, 2018.
Math Subject Classifications: 35J65, 35J25, 58E07.
Key Words: Ambrosetti-Prodi problem; degenerate potential;
topological degree; anisotropic continuous media.
Show me the PDF file (230 KB),
TEX file for this article.
 |
Dusan D. Repovs
Faculty of Education and Faculty of Mathematics and Physics
University of Ljubljana
SI-1000 Ljubljana, Slovenia
email: dusan.repovs@guest.arnes.si
|
|---|
Return to the EJDE web page
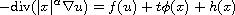
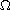 with homogeneous Neumann boundary
condition, where
with homogeneous Neumann boundary
condition, where
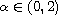 and f has a linear growth.
The main result establishes the existence of real numbers
and f has a linear growth.
The main result establishes the existence of real numbers
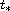 and
and
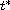 such that the problem has at least two solutions if
such that the problem has at least two solutions if
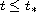 ,
there is
at least one solution if
,
there is
at least one solution if
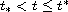 ,
and no solution exists
for all
,
and no solution exists
for all
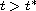 .
The proof combines a priori estimates with
topological degree arguments.
.
The proof combines a priori estimates with
topological degree arguments.
